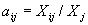Орлов А.И. Математика случая: Вероятность и статистика – основные факты: Семейство нормальных распределений

Семейство нормальных распределений

Введем понятие семейства нормальных распределений. По определению нормальным распределением называется распределение случайной величины Х, для которой распределение приведенной случайной величины есть Ф(х). Как следует из общих свойств масштабно-сдвиговых семейств распределений (см. выше), нормальное распределение – это распределение случайной величины

,

где Х – случайная величина с распределением Ф(Х), причем m = M(Y),  = D(Y). Нормальное распределение с параметрами сдвига m и масштаба  обычно обозначается N(m, ) (иногда используется обозначение N(m, )).

Как следует из (8), плотность вероятности нормального распределения N(m, ) есть

Нормальные распределения образуют масштабно-сдвиговое семейство. При этом параметром масштаба является d = 1/, а параметром сдвига c = - m/.

Для центральных моментов третьего и четвертого порядка нормального распределения справедливы равенства

Эти равенства лежат в основе классических методов проверки того, что результаты наблюдений подчиняются нормальному распределению. В настоящее время нормальность обычно рекомендуется проверять по критерию W Шапиро – Уилка. Проблема проверки нормальности обсуждается ниже.

Если случайные величины Х₁ и Х₂ имеют функции распределения N(m₁, ₁) и N(m₂, ₂) соответственно, то Х₁ + Х₂ имеет распределение  Следовательно, если случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(m, ), то их среднее арифметическое

имеет распределение N(m, ). Эти свойства нормального распределения постоянно используются в различных вероятностно-статистических методах принятия решений, в частности, при статистическом регулировании технологических процессов и в статистическом приемочном контроле по количественному признаку.