 Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Орлов А.И. Математика случая: Вероятность и статистика – основные факты: Гамма-распределения4. Случайные величины и их распределения Гамма-распределения Перейдем к семейству гамма-распределений. Они широко применяются в экономике и менеджменте, теории и практике надежности и испытаний, в различных областях техники, метеорологии и т.д. В частности, гамма-распределению подчинены во многих ситуациях такие величины, как общий срок службы изделия, длина цепочки токопроводящих пылинок, время достижения изделием предельного состояния при коррозии, время наработки до k-го отказа, k = 1, 2, …, и т.д. Продолжительность жизни больных хроническими заболеваниями, время достижения определенного эффекта при лечении в ряде случаев имеют гамма-распределение. Это распределение наиболее адекватно для описания спроса в экономико-математических моделях управления запасами (логистики). Плотность гамма-распределения имеет вид
Плотность вероятности в формуле (17) определяется тремя параметрами a, b, c, где a>0, b>0. При этом a является параметром формы, b - параметром масштаба и с - параметром сдвига. Множитель 1/Γ(а) является нормировочным, он введен, чтобы
Здесь Γ(а) - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (17),
При фиксированном а формула (17) задает масштабно-сдвиговое семейство распределений, порождаемое распределением с плотностью
Распределение вида (18) называется стандартным гамма-распределением. Оно получается из формулы (17) при b = 1 и с = 0. Частным случаем гамма-распределений при а = 1 являются экспоненциальные распределения (с λ = 1/b). При натуральном а и с=0 гамма-распределения называются распределениями Эрланга. С работ датского ученого К.А.Эрланга (1878-1929), сотрудника Копенгагенской телефонной компании, изучавшего в 1908-1922 гг. функционирование телефонных сетей, началось развитие теории массового обслуживания. Эта теория занимается вероятностно-статистическим моделированием систем, в которых происходит обслуживание потока заявок, с целью принятия оптимальных решений. Распределения Эрланга используют в тех же прикладных областях, в которых применяют экспоненциальные распределения. Это основано на следующем математическом факте: сумма k независимых случайных величин, экспоненциально распределенных с одинаковыми параметрами λ и с, имеет гамма-распределение с параметром формы а = k, параметром масштаба b = 1/λ и параметром сдвига kc. При с = 0 получаем распределение Эрланга. Если случайная величина X имеет гамма-распределение с параметром формы а таким, что d = 2a - целое число, b = 1 и с = 0, то 2Х имеет распределение хи-квадрат с d степенями свободы. Случайная величина X с гвмма-распределением имеет следующие характеристики: - математическое ожидание М(Х) = ab + c, - дисперсию D(X) = σ2 = ab2, - коэффициент вариации - асимметрию - эксцесс Нормальное распределение - предельный случай гамма-распределения. Точнее, пусть Z - случайная величина, имеющая стандартное гамма-распределение, заданное формулой (18). Тогда
для любого действительного числа х, где Ф(х) - функция стандартного нормального распределения N(0,1). В прикладных исследованиях используются и другие параметрические семейства распределений, из которых наиболее известны система кривых Пирсона, ряды Эджворта и Шарлье. Здесь они не рассматриваются. |
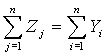 (17)
(17)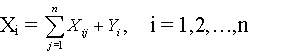
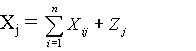 (18)
(18)