Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Орлов А.И. Математика случая: Вероятность и статистика – основные факты: Распределения Вейбулла - Гнеденко4. Случайные величины и их распределения Распределения Вейбулла - Гнеденко Экспоненциальные распределения - частный случай т. н. распределений Вейбулла - Гнеденко. Они названы по фамилиям инженера В. Вейбулла, введшего эти распределения в практику анализа результатов усталостных испытаний, и математика Б.В.Гнеденко (1912-1995), получившего такие распределения в качестве предельных при изучении максимального из результатов испытаний. Пусть Х - случайная величина, характеризующая длительность функционирования изделия, сложной системы, элемента (т.е. ресурс, наработку до предельного состояния и т.п.), длительность функционирования предприятия или жизни живого существа и т.д. Важную роль играет интенсивность отказа
где F(x) и f(x) - функция распределения и плотность случайной величины Х. Опишем типичное поведение интенсивности отказа. Весь интервал времени можно разбить на три периода. На первом из них функция λ(х) имеет высокие значения и явную тенденцию к убыванию (чаще всего она монотонно убывает). Это можно объяснить наличием в рассматриваемой партии единиц продукции с явными и скрытыми дефектами, которые приводят к относительно быстрому выходу из строя этих единиц продукции. Первый период называют "периодом приработки" (или "обкатки"). Именно на него обычно распространяется гарантийный срок. Затем наступает период нормальной эксплуатации, характеризующийся приблизительно постоянной и сравнительно низкой интенсивностью отказов. Природа отказов в этот период носит внезапный характер (аварии, ошибки эксплуатационных работников и т.п.) и не зависит от длительности эксплуатации единицы продукции. Наконец, последний период эксплуатации - период старения и износа. Природа отказов в этот период - в необратимых физико-механических и химических изменениях материалов, приводящих к прогрессирующему ухудшению качества единицы продукции и окончательному выходу ее из строя. Каждому периоду соответствует свой вид функции λ(х). Рассмотрим класс степенных зависимостей λ(х) = λ0bxb-1, (12) где λ0 > 0 и b > 0 - некоторые числовые параметры. Значения b < 1, b = 0 и b > 1 отвечают виду интенсивности отказов в периоды приработки, нормальной эксплуатации и старения соответственно. Соотношение (11) при заданной интенсивности отказа λ(х) - дифференциальное уравнение относительно функции F(x). Из теории дифференциальных уравнений следует, что
Подставив (12) в (13), получим, что
Распределение, задаваемое формулой (14) называется распределением Вейбулла - Гнеденко. Поскольку
где
то из формулы (14) следует, что величина а, задаваемая формулой (15), является масштабным параметром. Иногда вводят и параметр сдвига, т.е. функциями распределения Вейбулла - Гнеденко называют F(x - c), где F(x) задается формулой (14) при некоторых λ0 и b. Плотность распределения Вейбулла - Гнеденко имеет вид
где a > 0 - параметр масштаба, b > 0 - параметр формы, с - параметр сдвига. При этом параметр а из формулы (16) связан с параметром λ0 из формулы (14) соотношением, указанным в формуле (15). Экспоненциальное распределение - весьма частный случай распределения Вейбулла - Гнеденко, соответствующий значению параметра формы b = 1. Распределение Вейбулла - Гнеденко применяется также при построении вероятностных моделей ситуаций, в которых поведение объекта определяется "наиболее слабым звеном". Подразумевается аналогия с цепью, сохранность которой определяется тем ее звеном, которое имеет наименьшую прочность. Другими словами, пусть X1, X2,…, Xn - независимые одинаково распределенные случайные величины, X(1) = min (X1, X2,…, Xn), X(n) = max (X1, X2,…, Xn). В ряде прикладных задач большую роль играют X(1) и X(n), в частности, при исследовании максимально возможных значений ("рекордов") тех или иных значений, например, страховых выплат или потерь из-за коммерческих рисков, при изучении пределов упругости и выносливости стали, ряда характеристик надежности и т.п. Показано, что при больших n распределения X(1) и X(n), как правило, хорошо описываются распределениями Вейбулла - Гнеденко. Основополагающий вклад в изучение распределений X(1) и X(n) внес советский математик Б.В.Гнеденко. Использованию полученных результатов в экономике, менеджменте, технике и других областях посвящены труды В. Вейбулла, Э. Гумбеля, В.Б. Невзорова, Э.М. Кудлаева и многих иных специалистов. |
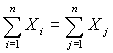 (13)
(13)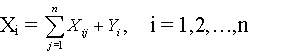 (14)
(14)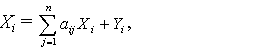 (16)
(16)