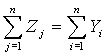Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Орлов А.И. Математика случая: Вероятность и статистика – основные факты: Экспоненциальные распределения4. Случайные величины и их распределения Экспоненциальные распределения Перейдем к другому семейству распределений, широко используемому в различных вероятностно-статистических методах принятия решений и других прикладных исследованиях, - семейству экспоненциальных распределений. Начнем с вероятностной модели, приводящей к таким распределениям. Для этого рассмотрим "поток событий", т.е. последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции; поток отказов оборудования в технологической цепочке; поток отказов изделий при испытаниях продукции; поток обращений клиентов в отделение банка; поток покупателей, обращающихся за товарами и услугами, и т.д. В теории потоков событий справедлива теорема, аналогичная центральной предельной теореме, но в ней речь идет не о суммировании случайных величин, а о суммировании потоков событий. Рассматривается суммарный поток, составленный из большого числа независимых потоков, ни один из которых не оказывает преобладающего влияния на суммарный поток. Например, поток вызовов, поступающих на телефонную станцию, слагается из большого числа независимых потоков вызовов, исходящих от отдельных абонентов. Доказано [6], что в случае, когда характеристики потоков не зависят от времени, суммарный поток полностью описывается одним числом
Это распределение называется экспоненциальным распределением, т.к. в формуле (10) участвует экспоненциальная функция e-λx. Величина 1/λ - масштабный параметр. Иногда вводят и параметр сдвига с, при этом экспоненциальным распределением называют распределение случайной величины Х + с, где распределение Х задается формулой (10). В формуле (10) е = 2,718281828… - основание натуральных логарифмов. Функция экспоненциального распределения F(x, λ) и его плотность f(x. λ) связаны простым соотношением
Это соотношение имеет простую интерпретацию в терминах теории надежности технических изделий и устройств. Оно означает, что интенсивность отказов (т.е. интенсивность выхода изделий из строя) постоянна, другими словами, не зависит от того, сколько времени изделие уже проработало. Обычно интенсивность отказов постоянна на основном этапе эксплуатации, после того, как на начальном этапе выявлены скрытые дефекты, и до того, как из-за естественного старения материалов начинает происходить ускоренный износ с резким возрастанием интенсивности выхода изделия из строя. |
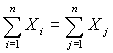 (10)
(10)