 Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
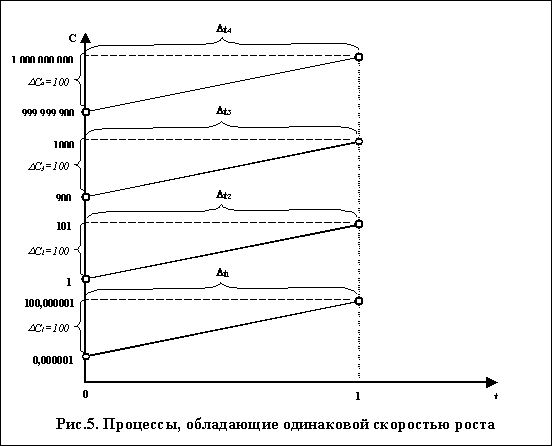
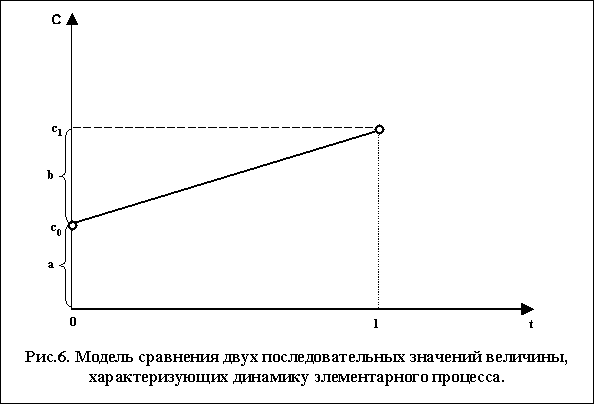
Галасюк В.. Галасюк В. Эффект «G-Гиперболизма» или как сравнивать несравнимоеТаким образом, результаты анализа сравнения величин X и Y на основе двух исходных типов критериев сравнения показывают, что оценки неравенства двух сравниваемых величин, осуществленные на основе критериев сравнения Эффект «G-гиперболизма» можно наглядно продемонстрировать с помощью следующего примера. Сравним между собой числа 100,000001 и 0,000001; 101 и 1; 1 000 и 900; 1 000 000 000 и 999 999 900, являющиеся последовательными значениями величин, характеризующих динамику четырех процессов, обладающих одинаковой скоростью роста (см. рис.5). Сравнивая числа каждой из четырех представленных пар между собой с помощью критерия Как известно, угловой коэффициент прямой равен тангенсу угла ее наклона, который в свою очередь вычисляется как отношение противолежащего катета к прилежащему, то есть b=∆С/∆t. Для каждой из прямых, представленных на рисунке 5, ∆С=DС1=DС2=DС3=DС4=100 и ∆t=∆t1=∆t2=∆t3=∆t4=1. Следовательно, для всех отрезков прямых, представленных на рисунке 5, угловой коэффициент b, отражающий скорость изменения численных значений, характеризующих процессы, одинаков. Таким образом, сравнение между собой чисел каждой из четырех представленных пар с помощью критерия Сравнение же чисел каждой из четырех представленных пар между собой с помощью критерия сравнения Возникает вопрос – какой из полученных четырех результатов сравнения величин X и Y можно считать «истинным»? Для ответа на поставленный вопрос проанализируем процесс сравнения двух величин на базе критерия сравнения Обозначим сравниваемые величины с0 и с1. Критерий сравнения Критерий сравнения Проанализировав содержание формул (1) и (2), нетрудно заметить, что единственным источником «G-гиперболизма» в них является отношение Таким образом, условия, при которых эффект «G-гиперболизма» не возникает, можно зафиксировать следующим образом: Из условий (3) следует вывод: эффект «G-гиперболизма» не возникает в двух случаях: при равенстве сравниваемых величин или при равенстве единице знаменателя критерия сравнения Следует отметить, что сравнение величин на базе критерия сравнения Для нейтрализации эффекта «G-гиперболизма» мы предлагаем ввести процедуру «G-нормализации». С учетом изложенного выше можно сделать вывод, что процедура «G-нормализации» может быть реализована либо путем приведения ситуации сравнения двух величин к условию с1=с0, либо к условию с0=1. Очевидно, что приведение ситуации сравнения любых двух величин к условию с1=с0, означающему равенство сравниваемых величин, с практической точки зрения нецелесообразно. Следовательно, процедуру «G-нормализации» целесообразно реализовать путем приведения ситуации сравнения двух величин к условию с0=1, означающему равенство единице знаменателя критерия сравнения Потенциально добиться равенства единице величины знаменателя критерия сравнения Второй способ – «способ параллельного переноса» – предполагает вычитание и из знаменателя и из числителя величины знаменателя, и последующее прибавление и к знаменателю и к числителю единицы, что, по сути, обеспечивает равенство единице знаменателя критерия сравнения (5) При реализации первого способа образуется замкнутый круг – осуществляется попытка решить проблему, возникающую при делении с помощью процедуры деления. Эффект «G-гиперболизма» не может быть нейтрализован при помощи деления, так как именно оно и порождает этот эффект. Следовательно, для нейтрализации эффекта «G-гиперболизма» может быть использован лишь второй способ – «способ параллельного переноса». Использование процедуры «G-нормализации» позволяет получить эталонную модель сравнения двух величин на базе критерия Проиллюстрируем изложенное выше на примере анализа динамики элементарного процесса, характеризуемого в определенные моменты времени величинами с0 и с1. Зафиксируем точки, соответствующие значениям этих величин на координатной плоскости. Учитывая, что ось времени введена условно, для удобства поставим в соответствие с0 и с1 значения t равные 0 и 1 соответственно. Тогда точки, отображенные на координатной плоскости, будут иметь координаты (0;с0) и (1;с1) соответственно (см. рис.6). Через указанные точки можно провести прямую, уравнение которой аналитически выражается следующим образом: где а – свободный член уравнения прямой; b – угловой коэффициент прямой;
t – значение аргумента. Используя формулу (6), величины с0 и с1 можно выразить следующим образом: Критерий сравнения Критерий сравнения Для рассматриваемой ситуации процедура «G-нормализации» предполагает осуществление следующего преобразования: Формула (11) аналитически выражает процедуру «G-нормализации», которая, по сути, заключается в параллельном переносе отрезка прямой, проходящего через точки, отражающие сравниваемые величины на координатной плоскости, обеспечивающем равенство единице знаменателя критерия сравнения Возвратимся к проиллюстрированному рисунком 5 примеру сравнения четырех пар чисел и применим процедуру «G-нормализации» для сравнения чисел каждой из четырех пар. Результат сравнения величин 100,000001 и 0,000001 на базе критерия То есть, несмотря на то, что сравнение чисел каждой из четырех представленных пар чисел между собой с помощью критерия сравнения Таким образом, мы приходим к выводу, о том, что только результат сравнения второй пары чисел ( Парадоксальность полученных результатов не позволяет остановиться на достигнутом в теоретическом отношении и указывает на необходимость дальнейших исследований эффекта «G-гиперболизма» и процедуры «G-нормализации». Ведь с точки зрения традиционной математики достаточно сложно представить, каким образом число 1 000 000 000 может быть больше числа 999 999 900 в 101 раз. Однако следует в полной мере отдавать себе отчет в том, что сама математика не является чем-то неизменным и созданным раз и навсегда. Наглядным примером служит существование помимо изучаемой в школе «традиционной» евклидовой геометрии, множества других геометрий: Гильберта, Римана, Лобачевского и др. На фоне «обычной» евклидовой геометрии, к которой мы привыкли, эти другие геометрии кажутся мягко говоря странными, хотя их непогрешимая логика ни в чем не уступает логике евклидовой геометрии. Как сказал Анри Пуанкаре: «Никакая геометрия не может быть более истинна, чем другая; та или иная геометрия может быть только более удобной» [9,с.41]. Поэтому следует признать, что евклидова геометрия используется наиболее часто, и ее позиции настолько сильны, что вряд ли можно ожидать в ближайшем будущем отказа от нее и перехода к использованию в повседневной деятельности, например, геометрии Лобачевского. Аналогичный вывод напрашивается в отношении использования традиционного сравнения при помощи процедуры деления и сравнения с применением процедуры «G-нормализации», нейтрализующей влияние эффекта «G-гиперболизма». Поэтому мы оставим более глубокое исследование процедуры «G-нормализации» и результатов ее применения на будущее. В теоретическом, методологическом и практическом аспектах фиксация и использование эффекта «G-гиперболизма» представляется нам чрезвычайно важной, поскольку эффект «G-гиперболизма» оказывает влияние на сравнение практически всех величин с использованием критерия сравнения В нашей следующей статье мы приведем примеры анализа ряда конкретных экономических ситуаций с учетом влияния эффекта «G-гиперболизма», а также представим модель «G-оптимизации», успешно используемую специалистами консалтинговой группы «КАУПЕРВУД» (www.cowperwood.dnepr.net). Список источников: 1. Галасюк В.В. Проблемы теории принятия экономических решений: Монография.- Днепропетровск: Новая идеология, 2002. – 304 стр. 2. Галасюк В.В. Про два вихідні типи критеріїв економічної ефективності затрат//Державний інформаційний бюллетень про приватизацію.-1999.-№ 9-С.78-80. 3. Галасюк В.В. О невозможности использования одного из двух исходных типов критериев экономической эффективности затрат//Государственный информационный бюллетень о приватизации.-2000.-№5.-С.78-80. 4. Галасюк В.В. Про неможливість побудови системи розрахунків з визначення економічної ефективності на підставі одного вихідного типу критеріїв//Державний інформаційний бюллетень про приватизацію.-2000.-№8.-С.77-79. 5. Галасюк В.В. Сколько должно быть исходных типов критериев экономической эффективности затрат?//Економіка: проблеми теорії та практики./Наука і освіта, Дніпропетровськ.-2000.-Випуск 34.-С.65-72. 6. 7. Галасюк В.В. Сколько должно быть исходных типов критериев экономической эффективности затрат: один, два, три…?//Фондовый рынок.-2000.-№3.-С.39-42. 8. Галасюк В.В. О двух исходных типах критериев экономической эффективности затрат//Вопросы оценки,Москва.-2000.-№1.-С.37-40. 9. Пуанкаре Анри. О науке: Пер. с франц.-М.-Наука. Главная редакция физико-математической литературы, 1983.-560 с. 20.10.2002 Посвящается Галасюк Марии Валерьевне в день ее однолетия. Зафиксировано Валерием Галасюком. |
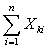 . (1)
. (1)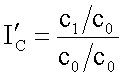 . (4)
. (4)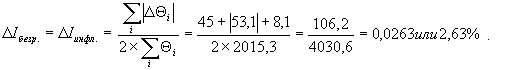 .
.
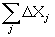 . (9)
. (9)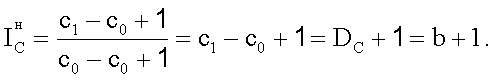 (11)
(11)