Недосекин А., Овсянко А. Нечетко-множественный подход в маркетинговых исследованиях

В самом общем случае функция треугольных чисел не есть треугольное число. Однако для большого разнообразия функций (как и для примера 2) функция принадлежности нечеткого числа A может быть приведена к треугольному виду, а сама нечеткая функция - признана треугольной.

Таким образом, мы получаем нечеткую функцию целевого параметра, приведенную к треугольному виду (например, объем продаж). В финансовом плане инвестиционного проекта этот параметр выступает уже как экзогенный, причем, поскольку в бизнес-плане бюджетирование проводится в дискретном времени, то вместо нечеткой функции финансовый план может использовать нечеткую последовательность объемов продаж, например, с поквартальной разбивкой. По аналогии с функциональной маркетинговой моделью мы заметим, что тогда точечные показатели эффективности инвестиционного проекта (скажем, чистая современная ценность проекта) являются треугольными нечеткими числами. Следовательно, можно решить задачу оценки риска инвестиций в подобный проект, как это сделано в [2].

Пример 3. Модель роста продаж продукции ЗАО "ABC"

Попробуем обобщить все изложенное на примере. Для ясности мы будем рассматривать конкретный проект, связанный с выводом на рынок новой марки потебительского товара – водки. Эта задача имеет свой предметный аналог, и ее результат может быть применим, например, для оценки эффективности инвестиционного проекта по созданию нового ликеро-водочного производства.

Рассмотрим ситуацию, сложившуюся с продажей алкогольных напитков в N-ском районе одной из областей Северо-Западного региона России. В силу отдаленности этого района от крупных производителей вино-водочной продукции эта продукция представлена на рынке N-ского района всего двумя секторами:

сектором продаж водки, производимой на местном ЗАО "АВС" (назовем этот сектор сектором АВС);

сектором продаж водки, производимой конкурентом ЗАО "АВС" - иногородней фирмой "Х". Назовем этот сектор сектором Х.

ЗАО "АВС" является новым предприятием, только что приступившим к выпуску алкогольной продукции. Однако оно имеет серьезные конкурентные преимущества перед фирмой Х, поскольку не несет глобальных транспортных затрат на ввоз водки в регион. Также ЗАО "АВС" может в ходе рекламной компании акцентировать свою "местную" принадлежность, призывая потребителя сделать выбор в пользу "своего", что даст региону дополнительные налоговые поступления и рабочие места. Такая сильная "патриотическая" имиджевая позиция, вкупе с облегченной структурой затрат, позволяет сделать вывод о том, что новая "местная" марка водки со временем серьезно потеснит продукцию сегмента Х. Остается оценить, какими темпами будет производиться это вытеснение.

Метод решения на основе четкой модели

Если мы зададимся наиболее ожидаемыми значениями экзогенных параметров, то будем решать нашу задачу в рамках четкой модели. Затем, размыв исходные параметры, мы перейдем к нечеткому описанию функции продаж.

Обозначим объем продаж в секторе АВС за L(t), млн л. в месяц, где t - номер месяца с момента начала наблюдения за рынком (начало продаж ЗАО "ABC"). Также обозначим объем продаж в секторе Х за K(t), млн. литров в месяц.

Тогда выполняется равенство

L(t) + K(t) = F(t) = F_max x d (t), (11)

где F(t) - суммарный объем продаж водки, F_max - предельное ожидаемое значение продаж в календарном году, d (t) - функция сезонности спроса. Согласно проведенным расчетам, предел продаж F_max - в обеих секторах рынка водки в N - ском районе составляет 3 млн. литров в месяц.

Сделаем допущения о функции сезонности спроса d (t). Она является периодической функцией с периодом один календарный год и принимает одни и те же значения по всему Северо-Западу России. Маркетологические исследования, ранее проведенные специалистами, дают табличный вид этой функции (см. табл. 2), если за t обозначить номер календарного месяца по порядку их следования (в общем случае номера t и t не совпадают):

Таблица 2

То есть, справедлива формула:

(12)

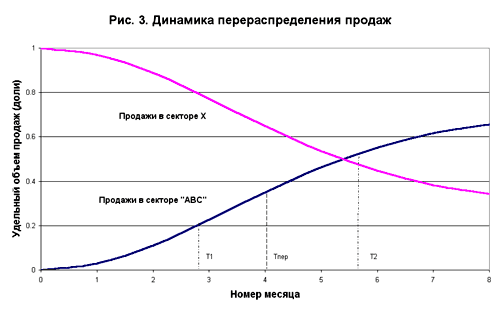
Для того, чтобы перейти к моделированию кривой продаж по ЗАО "ABC", необходимо перейти от сезонной зависимости продаж к внесезонной, учитывающей только перераспределение долей продаж между ЗАО и конкурентами. Разделим обе части равенства (11) на F(t). Тогда

j (t) + y (t) = 1, (13)

где j (t) = L(t) / F(t) - удельный объем (доля) продаж ЗАО "ABC", y (t) = K(t) / F(t) - то же для конкурентов. Качественный вид функций j и y см. рис. 3.

Поскольку функции j и y линейно зависимы, то в последующем мы будем рассматривать только динамику по ЗАО "ABC". Выдвинем основные допущения к качественному виду функции j :

1. Ясно, что по прошествии времени ЗАО "ABC" не останется единственным продавцом на рынке N-ского района, а достигнет некоего максимума продаж в долевом отношении. Как уже оговаривалось, мы не будем заниматься теоретическим вычислением вероятного значения этого макимума, и удовольствуветмся принятием целевого значения, определенного экспертным путем. Обозначим этот максимум j _max. В нашей задаче методом экспертных оценок определено наиболее ожидаемое значение j _max = 0.7.

Тогда мы можем строить модель j (t) в виде

j (t) = j _max  x R(t, r , b ), (14)

где R(t, r , b ) - профильная кривая, принимающая значения от 0 до 1, r - параметр формы, b - параметр масштаба.

2. Профильная кривая условно может быть сегментирована по оси абсцисс на три интервала:

а) интервал [0, Т1], соответствующий фазе начала продаж. Торговая марка еще неизвестна потребителю, однако она активно рекламируется. ЗАО вкладывает средства в развитие своей дилерской сети, проводит специализированные маркетинговые мероприятия по популяризации новой торговой марки (презентации, специальные праздничные скидки и проч.). Формируется элемент привыкания потребителя к новому продукту;

б) интервал [Т1, Т2], соответствующий фазе квазилинейного роста продаж. На этом этапе начинают окупаться усилия, вложенные в рекламную компанию. Торговая марка водки и ее производителя достигает возможного максимума "раскрученности", этот максимум соответствует точке перегиба профильной кривой R. Потребитель положительно оценил новый напиток и включил его в свой продуктовый набор, вытеснив из своего потребительского портфеля продукцию конкурентов;

в) интервал [Т2, inf], соответствующий фазе насыщения. В основном сформировался контингент, выбравший напиток новой марки для регулярного потребления. Приращение рекламного бюджета уже не приводит к адекватному росту рыночной доли. Если качество напитка со временем не меняется, то происходят лишь незначительные колебания спроса в сторону снижения или повышения, взаимно компенсирующие друг друга. Бесконечность в качестве верхней границы интервала выбрана условно. На самом деле, время наблюдения ограничено сроком жизни наблюдаемой торговой марки.

3. Таким образом, профильная кривая R характеризуется следующими количественными и качественными особенностями:

а) при t = 0 R = 0;

б) при t = inf  R = 1;

в) кривая R имеет точку перегиба (в этой точке вторая производная кривой R равна нулю).

Если бы новый товар не встречал сопротивления конкурентов в своем продвижении на рынок, тогда следовало бы искать функцию R в экспоненциальной или показательной форме, как это делается, например, в [1]. Но сопротивление вызывает перегиб функции, и ее приходится искать в двупараметрической форме. Одним из лучших приближений профильной кривой R, с учетом выдвинутых к ней требований, является кривая Вейбулла:

R(t, r , b ) = 1 - exp (- (t / b )^r ) (15)

с параметром формы r = 2 (такое значение параметра r обеспечивает кривой R приемлемую гладкость). Чем больше значение b , тем медленнее будут нарастать продажи ЗАО.

Чтобы определить значение параметра b , необходимо задаться координатой одной из характерных точек на кривой R. В качестве такой точки может служить момент времени, когда новая торговая марка займет порядка 50% от своего предельного долевого уровня на региональном рынке (R = 0.5, j (Т_пер) = j _max /2 = 0.35). Этому значению соответствует момент Т_пер, который определяется по нетрудно выводимой на основе (15) формуле при r = 2:

, (16)

откуда получаем значение b :

. (17)

Опять же методом экспертного опроса был определен параметр Т_пер, и его наиболее ожидаемое значение составило 4 месяца.

В итоге, результирующее оценочное значение уровня продаж ЗАО "ABC" во времени, с учетом всего изложенного, составляет:

L(t) = F_max x d (t) x j _max  x (1 - exp (- (t / b )^r ), (18)

где d (t) определяется (12) и таблицей 2, r = 2, а b вычисляется по (17) и составляет 4.8 месяца.

Пусть предприятие "АВС" начинает продажи в апреле 2000 года, т.е. смещение между номерами календарных месяцев t и номерами месяцев наблюдения составляет 4. Проведем расчеты по формулам (12) - (18). Результаты расчетов сведены в таблицу 3.

Таблица 3

Таким образом, целью специальных маркетинговых исследований по рынку водки в N-ском районе может быть определение следующих трех экзогенных параметров модели продаж:

1. F_max - предельный размер рынка водок данного класса в N-ском районе, млн. л в месяц.

2. j _max - предельно достигаемая доля ЗАО "ABC" на рынке водок данного класса, %.

3. Т_пер - срок, за который торговая марка ЗАО "ABC" займет 50% от своего предельного уровня на региональном рынке, месяцев.

Также в качестве экзогенного параметра модели выступает вектор сезонности спроса d (t). А целевым параметором модели является натуральный объем продаж водки "АВС", причем в качестве самой модели выступает функциональное соотношение (18).

Теперь, чтобы адекватно учесть фактор приближенности экспертных оценок, осуществим замещение четкой модели нечеткой, с заменой точных значений экзогенных параметров нечеткими числами.

Трансформация решения задачи с помощью нечетких функций

Мы не можем совершенно конструктивно оценить степень точности, с которой эксперты достигают своих количественных оценок рынка. Однако мы можем задаться расчетным параметром l степени "размытия", степени нечеткости модели. Чем больше l , тем шире расчетный диапазон экзогенных параметров, тем шире и расчетный диапазон нечеткой функции целевого параметра модели. Когда модель будет построена до конца, т.е. до оценки риска инвестиций, исследователь может оценить степень риска инвестиционного решения в зависимости от степени нечеткости исходных данных - и тем самым проанализировать устойчивость принимаемого решения к исходной информационной неопределенности.

Итак, замещаем в модели точные экзогенные параметры вектора А на треугольные нечеткие числа вида (А x (1 - l ), А, А x (1 + l )). Пусть, для примера, степень нечеткости модели составляет 20%. Тогда расчет минимальных, ожидаемых и максимальных значений функции L(t) сведен в таблицу 4.

Таблица 4

Если мы договорились привести функцию L(t) к треугольному виду, то таблица 4 содержит конструктивное описание этой функции. Если договоренности о подобной аппроксимации нет, необходим требуемый уровень дискретизации оси времени и соответствующая экстраполяция параметров функций принадлежности в промежуточных точках.

Заключение

Без ложной скромности осмеливаемся заявить свое первенство в приложении математики нечетких множеств к задачам маркетингового моделирования. Здесь математика подобного рода, как и вообще в экономических задачах, оказывается как нельзя более кстати. Субъективные вероятности, прежде широко применяемые в экономическом анализе, сегодня встречают серьезные теоретические препятствия в использовании. В частности, подвергается сомнению безусловное применение критерия максимума энтропии Гиббса-Джейнса, лежащего в основе обоснования наиболее правдоподобных вероятностных распределений (подробнее об этом в [4]). Нечетко-множественный подход не сталкивается с затруднениями подобного рода. Он имеет дело не с возможностью, а с ожидаемостью. Он опирается на интуитивное знание исследователя рынка об ожидаемом диапазоне разброса экзогенных параметров. И если исходная неопределенность описана исследователем адекватно, в форме ожидаемых интервальных диапазонов, тогда оценка разброса целевых параметров модели, базирующася на применении обоснованных здесь нечетких функций и последовательностей, становится только делом техники.

© 1999 Алексей Недосекин, Антон Овсянко,
КГ "Воронов и Максимов"

Литература

1. Lilien G., Kotler Ph. Marketing Decision Making: A Model-Building Approach. N.Y.: Harper & Row Publishers, 1983.
2. Недосекин А.О. Применение теории нечетких множеств к задачам управления финансами // Аудит и финансовый анализ, 2000, № 2.
3. Кофман А., Хил Алуха Х. Введение теории нечетких множеств в управлении предприятиями. Минск, Вышэйшая школа, 1992.
4. Смоляк С.А. Учет специфики инвестиционных проектов при оценке их эффективности // Аудит и финансовый анализ, 1999, №3.