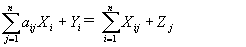Орлов А.И. Математика случая: Вероятность и статистика – основные факты: Математическое ожидание

Математическое ожидание

Рассмотрим  случайную величину с числовыми значениями. Часто оказывается полезным связать с этой функцией число – ее «среднее значение» или, как говорят, «среднюю величину», «показатель центральной тенденции». По ряду причин, некоторые из которых будут ясны из дальнейшего, в качестве «среднего значения» обычно используют математическое ожидание.

Определение 3. Математическим ожиданием случайной величины Х называется число

   (4)

т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.

Пример 6. Вычислим математическое ожидание числа, выпавшего на верхней грани игрального кубика. Непосредственно из определения 3 следует, что

Утверждение 2. Пусть случайная величина Х принимает значения х₁, х₂,…, х_m. Тогда справедливо равенство

   (5)

т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям того, что случайная величина принимает определенные значения.

В отличие от (4), где суммирование проводится непосредственно по элементарным событиям, случайное событие  может состоять из нескольких элементарных событий.

Иногда соотношение (5) принимают как определение математического ожидания. Однако с помощью определения 3, как показано далее, более легко установить свойства математического ожидания, нужные для построения вероятностных моделей реальных явлений, чем с помощью соотношения (5).

Для доказательства соотношения (5) сгруппируем в (4) члены с одинаковыми значениями случайной величины :

Поскольку постоянный множитель можно вынести за знак суммы, то

По определению вероятности события

С помощью двух последних соотношений получаем требуемое:

Понятие математического ожидания в вероятностно-статистической теории соответствует понятию центра тяжести в механике. Поместим в точки х₁, х₂,…, х_m на числовой оси массы P(X=x₁), P(X=x₂),…, P(X=x_m) соответственно. Тогда равенство (5) показывает, что центр тяжести этой системы материальных точек совпадает с математическим ожиданием, что показывает естественность определения 3.

Утверждение 3. Пусть Х – случайная величина, М(Х) – ее математическое ожидание, а – некоторое число. Тогда

1) М(а)=а; 2) М(Х-М(Х))=0; 3) М[(X-a)²]=M[(X-M(X))²]+(a-M(X))².

Для доказательства рассмотрим сначала случайную величину, являющуюся постоянной,  т.е. функция  отображает пространство элементарных событий  в единственную точку а. Поскольку постоянный множитель можно выносить за знак суммы, то

Если каждый член суммы разбивается на два слагаемых, то и вся сумма разбивается на две суммы, из которых первая составлена из первых слагаемых, а вторая – из вторых. Следовательно, математическое ожидание суммы двух случайных величин Х+У, определенных на одном и том же пространстве элементарных событий, равно сумме математических ожиданий М(Х) и М(У) этих случайных величин:

М(Х+У) = М(Х) + М(У).

А потому М(Х-М(Х)) = М(Х) - М(М(Х)). Как показано выше, М(М(Х)) = М(Х). Следовательно, М(Х-М(Х)) = М(Х) - М(Х) = 0.

Поскольку (Х - а)² = {(X – M(X)) + (M(X) - a)}² = (X - M(X))² + 2(X - M(X))(M(X) - a) + (M(X) – a)², то M[(Х - а)²] =M(X - M(X))² + M{2(X - M(X))(M(X) - a)} +M[(M(X) – a)²]. Упростим последнее равенство. Как показано в начале доказательства утверждения 3, математическое ожидание константы – сама эта константа, а потому M[(M(X) – a)²] = (M(X) – a)². Поскольку постоянный множитель можно выносить за знак суммы, то M{2(X - M(X))(M(X) - a)} = 2(M(X) - a)М(X - M(X)). Правая часть последнего равенства равна 0, поскольку, как показано выше, М(Х-М(Х))=0. Следовательно, М[(X-a)²]=M[(X-M(X))²]+(a-M(X))², что и требовалось доказать.

Из сказанного вытекает, что М[(X-a)²] достигает минимума по а, равного M[(X-M(X))²], при а = М(Х), поскольку второе слагаемое в равенстве 3) всегда неотрицательно и равно 0 только при указанном значении а.

Утверждение 4. Пусть случайная величина Х принимает значения х₁, х₂,…, х_m, а f – некоторая функция числового аргумента. Тогда

Для доказательства сгруппируем в правой части равенства (4), определяющего математическое ожидание, члены с одинаковыми значениями :

Пользуясь тем, что постоянный множитель можно выносить за знак суммы, и определением вероятности случайного события (2), получаем

что и требовалось доказать.

Утверждение 5. Пусть Х и У – случайные величины, определенные на одном и том же пространстве элементарных событий, а и b – некоторые числа. Тогда M(aX+bY)=aM(X)+bM(Y).

С помощью определения математического ожидания и свойств символа суммирования получаем цепочку равенств:

Требуемое доказано.

Выше показано, как зависит математическое ожидание от перехода к другому началу отсчета и к другой единице измерения (переход Y=aX+b), а также к функциям от случайных величин. Полученные результаты постоянно используются в технико-экономическом анализе, при оценке финансово-хозяйственной деятельности предприятия, при переходе от одной валюты к другой во внешнеэкономических расчетах, в нормативно-технической документации и др. Рассматриваемые результаты позволяют применять одни и те же расчетные формулы при различных параметрах масштаба и сдвига.