 Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Орлов А.И. Математика случая: Вероятность и статистика – основные факты: Независимые испытания2. Основы теории вероятностей Независимые испытания В вероятностных моделях процедур принятия решений с помощью понятия независимости событий можно придать точный смысл понятию «независимые испытания». Для этого рассмотрим сложный опыт, состоящий в проведении двух испытаний. Эти испытания называются независимыми, если любые два события А и В, из которых А определяется по исходу первого испытания, а В – по исходу второго, являются независимыми. Пример 4. Опишем вероятностное пространство, соответствующее бросанию двух монет независимо друг от друга. Разбор примера. Пространство элементарных событий состоит из четырех элементов: ГГ, ГР, РГ, РР (запись ГГ означает, что первая монета выпала гербом и вторая – тоже гербом; запись РГ – первая – решеткой, а вторая – гербом, и т.д.). Поскольку события «первая монета выпала решеткой» и «вторая монета выпала гербом» являются независимыми по определению независимых испытаний и вероятность каждого из них равна ½, то вероятность РГ равна ¼. Аналогично вероятность каждого из остальных элементарных событий также равна ¼. Пример 5. Опишем вероятностное пространство, соответствующее проверке качества двух единиц продукции независимо друг от друга, если вероятность дефектности равна х. Разбор примера. Пространство элементарных событий состоит из четырех элементов: Вероятность того, что единица продукции дефектна, есть х, а потому вероятность того, что имеет место противоположное событие, т.е. единица продукции годна, есть 1 – х. Поскольку результат проверки первой единицы продукции не зависит от такового для второй, то |
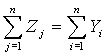 (1)
(1)