 Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Теория принятия решений: Интервальные данные в задачах оценивания параметров (на примере гамма-распределения)2.3.4. Интервальные данные в задачах оценивания параметров (на примере гамма-распределения) Рассмотрим классическую в прикладной математической статистике параметрическую задачу оценивания. Исходные данные – выборка x1 , x2 , ..., xn, состоящая из n действительных чисел. В вероятностной модели простой случайной выборки ее элементы x1 , x2 , ..., xn считаются набором реализаций n независимых одинаково распределенных случайных величин. Будем считать, что эти величины имеют плотность f(x). В параметрической статистической теории предполагается, что плотность f(x) известна с точностью до конечномерного параметра, т.е., Все результаты наблюдений определяются с некоторой точностью, в частности, записываются с помощью конечного числа значащих цифр (обычно 2 – 5). Следовательно, все реальные распределения результатов наблюдений дискретны. Обычно считают, что эти дискретные распределения достаточно хорошо приближаются непрерывными. Уточняя это утверждение, приходим к уже рассматривавшейся модели, согласно которой статистику доступны лишь величины yj = xj + где xi – «истинные» значения, образуют простую случайную выборку из некоторого двумерного распределения, причем x1 , x2 , ..., xn - выборка из распределения с плотностью Пусть Изложение ниже идет на примере оценивания параметров гамма-распределения, хотя аналогичные результаты можно получить и для других параметрических семейств, а также для задач проверки гипотез (см. ниже) и т.д. Наша цель – продемонстрировать основные черты подхода статистики интервальных данных. Его разработка была стимулирована подготовкой ГОСТ 11.011-83 [4]. Отметим, что постановки статистики объектов нечисловой природы соответствуют подходу, принятому в общей теории устойчивости [3,27]. В соответствии с этим подходом выборке x = (x1 , x2 , ..., xn ) ставится в соответствие множество допустимых отклонений G(x), т.е. множество возможных значений вектора результатов наблюдений y = (y1 , y2 , ..., yn ). Если известно, что абсолютная погрешность результатов измерений не превосходит Если известно, что относительная погрешность не превосходит Теория устойчивости позволяет учесть «наихудшие» отклонения, т.е. приводит к выводам типа минимаксных, в то время как конкретные модели погрешностей позволяют делать заключения о поведении статистик «в среднем». Оценки параметров гамма-распределения. Как известно, случайная величина Х имеет гамма-распределение, если ее плотность такова [4]: где a – параметр формы, b – параметр масштаба, Поскольку M(X) = ab, D(X) = ab2, то оценки метода имеют вид где с точностью до бесконечно малых более высокого порядка. Оценка максимального правдоподобия a* имеет вид [4]: где При больших n с точностью до бесконечно малых более высокого порядка Как и для оценок метода моментов, оценка максимального правдоподобия b* параметра масштаба имеет вид При больших n с точностью до бесконечно малых более высокого порядка Используя свойства гамма-функции, можно показать [4], что при больших а с точностью до бесконечно малых более высокого порядка. Сравнивая с формулами (11), убеждаемся в том, что средние квадраты ошибок для оценок метода моментов больше соответствующих средних квадратов ошибок для оценок максимального правдоподобия. Таким образом, с точки зрения классической математической статистики оценки максимального правдоподобия имеют преимущество по сравнению с оценками метода моментов. Необходимость учета погрешностей измерений. Положим Из свойств функции В силу состоятельности оценки максимального правдоподобия a* из формулы (13) следует, что Согласно модели статистики интервальных данных результатами наблюдений являются не xi , а yi, вместо v по реальным данным рассчитывают Имеем В силу закона больших чисел при достаточно малой погрешности по вероятности (в предположении, что все погрешности одинаково распределены). Таким образом, наличие погрешностей вносит сдвиг, вообще говоря, не исчезающий при росте объема выборки. Следовательно, если где величина a*(y) определена по формуле (12) с заменой xi на yi, i=1,2,…,n. Из формулы (13) следует [4], что т.е. влияние погрешностей измерений увеличивается по мере роста а. Из формул для v и w следует, что с точностью до бесконечно малых более высокого порядка С целью нахождения асимптотического распределения w выделим, используя формулу (16) и формулу для v, главные члены в соответствующих слагаемых Таким образом, величина w представлена в виде суммы независимых одинаково распределенных случайных величин (с точностью до зависящего от случая остаточного члена порядка 1/n). В каждом слагаемом выделяются две части – одна, соответствующая Мб и вторая, в которую входят Из асимптотического совпадения дисперсий v и w, вида параметров асимптотического распределения (при Соотношение (18) уточняет утверждение о несостоятельности a*. Из него следует также, что не имеет смысла безгранично увеличивать объем выборки n с целью повышения точности оценивания параметра а, поскольку при этом уменьшается только второе слагаемое в (18), а первое остается постоянным. В соответствии с общим подходом статистики интервальных данных в стандарте [4] предлагается определять рациональный объем выборки nrat определять из условия «уравнивания погрешностей» (предложено в монографии [3]) различных видов в формуле (18), т.е. из условия Упрощая это уравнение в предположении Согласно сказанному выше, целесообразно использовать лишь выборки с объемами Применение методов теории устойчивости. Найдем асимптотическую нотну. Как следует из вида главного линейного члена в формуле (17), решение оптимизационной задачи соответствующей ограничениям на абсолютные погрешности, имеет вид Однако при этом пары при a>1, где Таким образом, с точностью до бесконечно малых более высокого порядка нотна имеет вид Применим полученные результаты к построению доверительных интервалов. В постановке классической математической статистики (т.е. при где В постановке статистики интервальных данных (т.е. при где в вероятностной постановке (пары Если ограничения наложены на предельную относительную погрешность, задана величина (I) Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых. (II) Относительная погрешность произведения и частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя. Можно показать, что в рамках статистики интервальных данных с ограничениями на относительную погрешность правила (I) и (II) являются строгими утверждениями при Обозначим относительную погрешность некоторой величины t через ОП(t), абсолютную погрешность – через АП(t). Из правила (I) следует, что ОП( Поскольку рассмотрения ведутся при по вероятности при Поскольку при справедливости (19) с точностью до бесконечно малых более высокого порядка то с помощью трех последних соотношений имеем Применим еще одно правило приближенных вычислений [32, с.142]. (III) Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей слагаемых. Из (20) и правила (III) следует, что Из (15) и (21) вытекает [4, с.44, ф-ла (18)], что откуда в соответствии с ранее полученной формулой для рационального объема выборки с заменой В частности, при a = 5,00, В соответствии с ранее проведенными рассмотрениями асимптотический доверительный интервал для a, соответствующий доверительной вероятности В частности, при При больших а в силу соображений, приведенных при выводе формулы (19), можно связать между собой относительную и абсолютную погрешности результатов наблюдений xi : Следовательно, при больших а имеем Таким образом, проведенные рассуждения дали возможность вычислить асимптотику интеграла, задающего величину А. Сравнение методов оценивания. Изучим влияние погрешностей измерений (с ограничениями на абсолютную погрешность) на оценку Погрешность s2 зависит от способа вычисления s2. Если используется формула то необходимо использовать соотношения По сравнению с анализом влияния погрешностей на оценку а* здесь возникает новый момент – необходимость учета погрешностей в случайной составляющей отклонения оценки тогда Если вычислять s2 по формуле то аналогичные вычисления дают, что т.е. погрешность при больших а существенно больше. Хотя правые части формул (22) и (24) тождественно равны, но погрешности вычислений по этим формулам весьма отличаются. Связано это с тем, что в формуле (24) последняя операция – нахождение разности двух больших чисел, примерно равных по величине (для выборки из гамма-распределения при большом значении параметра формы). Из полученных результатов следует, что При выводе этой формулы использована линеаризация влияния погрешностей (выделение главного линейного члена). Используя связь (21) между абсолютной и относительной погрешностями, можно записать Эта формула отличается от приведенной в [4, с.44, ф-ла (19)] поскольку в [4] вместо (23) использовалась оценка Используя соотношение (23), мы характеризуем влияние погрешностей «в среднем». Доверительный интервал, соответствующий доверительной вероятности 0,95, имеет вид Если Необходимо выбрать способ сравнения двух методов оценивания параметра а, поскольку в длины доверительных интервалов входят две составляющие – зависящая от доверительной вероятности и не зависящая от нее. Выберем а оценке Ясно, что больших а или больших n справедливо неравенство Из (25) и (26) элементарными преобразованиями получаем следующее правило принятия решений. Если то Пример анализа реальных данных опубликован в [4]. На основе рассмотрения проблем оценивания параметров гамма-распределения можно сделать некоторые общие выводы. Если в классической теории математической статистики: а) существуют состоятельные оценки an параметра а, б) для повышения точности оценивания объем выборки целесообразно безгранично увеличивать; в) оценки максимального правдоподобия лучше оценок метода моментов, то в статистике интервальных данных, учитывающей погрешности измерений, соответственно: а) не существует состоятельных оценок: для любой оценки an существует константа с такая, что б) не имеет смысла рассматривать объемы выборок, большие «рационального объема выборки» в) оценки метода моментов в обширной области параметров Ясно, что приведенные выше результаты справедливы не только для рассмотренной задачи оценивания параметров гамма-распределения, но и для многих других постановок прикладной математической статистики. Метрологические, методические, статистические и вычислительные погрешности. Целесообразно выделить ряд видов погрешностей статистических данных. Погрешности, вызванные неточностью измерения исходных данных, называем метрологическими. Их максимальное значение можно оценить с помощью нотны. Впрочем, выше на примере оценивания параметров гамма-распределения показано, что переход от максимального отклонения к реально имеющемуся в вероятностно-статистической модели не меняет выводы (с точностью до умножения предельных значений погрешностей Методические погрешности вызваны неадекватностью вероятностно-статистической модели, отклонением реальности от ее предпосылок. Неадекватность обычно не исчезает при росте объема выборки. Методические погрешности целесообразно изучать с помощью «общей схемы устойчивости» [3,27], обобщающей популярную в теории робастных статистических процедур модель засорения большими выбросами. В настоящей главе методические погрешности не рассматриваются. Статистическая погрешность – это та погрешность, которая традиционно рассматривается в математической статистике. Ее характеристики – дисперсия оценки, дополнение до 1 мощности критерия при фиксированной альтернативе и т.д. Как правило, статистическая погрешность стремится к 0 при росте объема выборки. Вычислительная погрешность определяется алгоритмами расчета, в частности, правилами округления. На уровне чистой математики справедливо тождество правых частей формул (22) и (24), задающих выборочную дисперсию s2, а на уровне вычислительной математики формула (22) дает при определенных условиях существенно больше верных значащих цифр, чем вторая [34, с.51-52]. Выше на примере задачи оценивания параметров гамма-распределения рассмотрено совместное действие метрологических и вычислительных погрешностей, причем погрешности вычислений оценивались по классическим правилам для ручного счета [32]. Оказалось, что при таком подходе оценки метода моментов имеют преимущество перед оценками максимального правдоподобия в обширной области изменения параметров. Однако, если учитывать только метрологические погрешности, как это делалось выше в примерах 1-5, то с помощью аналогичных выкладок можно показать, что оценки этих двух типов имеют (при достаточно больших n) одинаковую погрешность. Вычислительную погрешность здесь подробно не рассматриваем. Ряд интересных результатов о ее роли в статистике получили Н.Н.Ляшенко и М.С.Никулин [35]. |
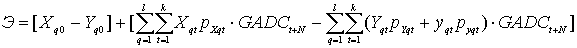
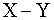
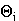
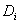
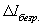
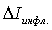 (14)
(14)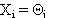
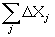 (16)
(16)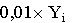 . (17)
. (17)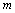
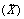
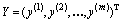
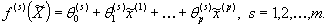
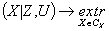
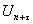
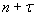 (20)
(20)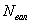 (22)
(22)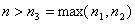 (24)
(24)
