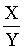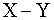Теория принятия решений: Современное состояние прикладной статистики (типовые практические задачи и методы их решения)

2.2. Вероятностно-статистические методы описания неопределенностей в теории принятия решений

2.2.6. Современное состояние прикладной статистики (типовые практические задачи и методы их решения)

 Статистические данные и прикладная статистика. Под прикладной статистикой понимают часть математической статистики, посвященную методам обработки реальных статистических данных, а также соответствующее математическое и программное обеспечение. Таким образом, чисто математические задачи не включают в прикладную статистику.

 Под статистическими данными понимают числовые или нечисловые значения контролируемых параметров (признаков) исследуемых объектов, которые получены в результате наблюдений (измерений, анализов, испытаний, опытов и т.д.) определенного числа признаков, у каждой единицы, вошедшей в исследование. Способы получения статистических данных и объемы выборок устанавливают, исходя из постановок конкретной прикладной задачи на основе методов математической теории планирования эксперимента.

 Результат наблюдения x_i исследуемого признака Х (или совокупности исследуемых признаков Х) у i – ой единицы выборки отражает количественные и/или качественные свойства обследованной единицы с номером i (здесь i = 1, 2, … , n, где n – объем выборки). Деление прикладной статистики на направления соответственно виду обрабатываемых результатов наблюдений (т.е. на статистику случайных величин, многомерный статистический анализ, статистику временных рядов и статистику объектов нечисловой природы) обсуждалось выше.

 Результаты наблюдений x₁, x₂,…, x_n, где x_i – результат наблюдения i – ой единицы выборки, или результаты наблюдений для нескольких выборок, обрабатывают с помощью методов прикладной статистики, соответствующих поставленной задаче. Используют, как правило, аналитические методы, т.е. методы, основанные на численных расчетах (объекты нечисловой природы при этом описывают с помощью чисел). В отдельных случаях допустимо применение графических методов (визуального анализа).

 Количество разработанных к настоящему времени методов обработки данных весьма велико. Они описаны в сотнях тысяч книг и статей, а также в стандартах и других нормативно-технических и инструктивно-методических документах.

 Многие методы прикладной статистики требуют проведения трудоемких расчетов, поэтому для их реализации необходимо использовать компьютеры. Программы расчетов на ЭВМ должны соответствовать современному научному уровню. Однако для единичных расчетов при отсутствии соответствующего программного обеспечения успешно используют микрокалькуляторы.

 Задачи статистического анализа точности и стабильности технологических процессов и качества продукции. Статистические методы используют, в частности, для анализа точности и стабильности технологических процессов и качества продукции. Цель - подготовка решений, обеспечивающих эффективное функционирование технологических единиц и повышение качества и конкурентоспособности выпускаемой продукции. Статистические методы следует применять во всех случаях, когда по результатам ограниченного числа наблюдений требуется установить причины улучшения или ухудшения точности и стабильности технологического оборудования. Под точностью технологического процесса понимают свойство технологического процесса, обусловливающее близость действительных и номинальных значений параметров производимой продукции. Под стабильностью технологического процесса понимают свойство технологического процесса, обусловливающее постоянство распределений вероятностей для его параметров в течение некоторого интервала времени без вмешательства извне.

 Целями применения статистических методов анализа точности и стабильности технологических процессов и качества продукции на стадиях разработки, производства и эксплуатации (потребления) продукции являются, в частности:

• определение фактических показателей точности и стабильности технологического процесса, оборудования или качества продукции;

• установление соответствия качества продукции требованиям нормативно-технической документации;

• проверка соблюдения технологической дисциплины;

• изучение случайных и систематических факторов, способных привести к появлению дефектов;

• выявление резервов производства и технологии;

• обоснование технических норм и допусков на продукцию;

• оценка результатов испытаний опытных образцов при обосновании требований к продукции и нормативов на нее;

• обоснование выбора технологического оборудования и средств измерений и испытаний;

• сравнение различных образцов продукции;

• обоснование замены сплошного контроля статистическим;

• выявление возможности внедрения статистических методов управления качеством продукции, и т.д.

 Для достижения перечисленных выше целей применяют различные методы описания данных, оценивания и проверки гипотез. Приведем примеры постановок задач.

 Задачи одномерной статистики (статистики случайных величин). Сравнение математических ожиданий проводят в тех случаях, когда необходимо установить соответствие показателей качества изготовленной продукции и эталонного образца. Это – задача проверки гипотезы:

Н₀: М(Х) = m₀,

где m₀ – значение соответствующее эталонному образцу; Х – случайная величина, моделирующая результаты наблюдений. В зависимости от формулировки вероятностной модели ситуации и альтернативной гипотезы сравнение математических ожиданий проводят либо параметрическими, либо непараметрическими методами.

 Сравнение дисперсий проводят тогда, когда требуется установить отличие рассеивания показателя качества от номинального. Для этого проверяют гипотезу:

 Ряд иных постановок задач одномерной статистики приведен ниже. Не меньшее значение, чем задачи проверки гипотез, имеют задачи оценивания параметров. Они, как и задачи проверки гипотез, в зависимости от используемой вероятностной модели ситуации делятся на параметрические и непараметрические.

 В параметрических задачах оценивания принимают вероятностную модель, согласно которой результаты наблюдений x₁, x₂,…, x_n рассматривают как реализации n независимых случайных величин с функцией распределения F(x;θ). Здесь θ – неизвестный параметр, лежащий в пространстве параметров Θ заданном используемой вероятностной моделью. Задача оценивания состоит в определении точечной оценок и доверительных границ (либо доверительной области) для параметра θ.

Параметр θ – либо число, либо вектор фиксированной конечной размерности. Так, для нормального распределения θ = (m, σ²) – двумерный вектор, для биномиального θ = p – число, для гамма-распределения θ = (a, b, c) – трехмерный вектор, и т.д.

 В современной математической статистике разработан ряд общих методов определения оценок и доверительных границ – метод моментов, метод максимального правдоподобия, метод одношаговых оценок, метод устойчивых (робастных) оценок, метод несмещенных оценок и др. Кратко рассмотрим первые три из них. Теоретические основы различных методов оценивания и полученные с их помощью конкретные правила определения оценок и доверительных границ для тех или иных параметрических семейств распределений рассмотрены в специальной литературе, включены в нормативно-техническую и инструктивно-методическую документацию.

 Метод моментов основан на использовании выражений для моментов рассматриваемых случайных величин через параметры их функций распределения. Оценки метода моментов получают, подставляя выборочные моменты вместо теоретических в функции, выражающие параметры через моменты.

 В методе максимального правдоподобия, разработанном в основном Р.А.Фишером, в качестве оценки параметра θ берут значение θ*, для которого максимальна так называемая функция правдоподобия

f(x₁, θ) f(x₂, θ) … f(x_n, θ),

где x₁, x₂,…, x_n - результаты наблюдений; f(x, θ) – их плотность распределения, зависящая от параметра θ, который необходимо оценить.

 Оценки максимального правдоподобия, как правило, эффективны (или асимптотически эффективны) и имеют меньшую дисперсию, чем оценки метода моментов. В отдельных случаях формулы для них выписываются явно (нормальное распределение, экспоненциальное распределение без сдвига). Однако чаще для их нахождения необходимо численно решать систему трансцендентных уравнений (распределения Вейбулла-Гнеденко, гамма). В подобных случаях целесообразно использовать не оценки максимального правдоподобия, а другие виды оценок, прежде всего одношаговые оценки. В литературе их иногда не вполне точно называют «приближенные оценки максимального правдоподобия». При достаточно больших объемах выборок они имеют столь же хорошие свойства, как и оценки максимального правдоподобия. Поэтому их следует рассматривать не как «приближенные», а как оценки, полученные по другому методу, не менее обоснованному и эффективному, чем метод максимального правдоподобия. Одношаговые оценки вычисляют по явным формулам [14].

 В непараметрических задачах оценивания принимают вероятностную модель, в которой результаты наблюдений x₁, x₂,…, x_n рассматривают как реализации n независимых случайных величин с функцией распределения F(x) общего вида. От F(x) требуют лишь выполнения некоторых условий типа непрерывности, существования математического ожидания и дисперсии и т.п. Подобные условия не являются столь жесткими, как условие принадлежности к определенному параметрическому семейству.

 В непараметрической постановке оценивают либо характеристики случайной величины (математическое ожидание, дисперсию, коэффициент вариации), либо ее функцию распределения, плотность и т.п. Так, в силу закона больших чисел выборочное среднее арифметическое  является состоятельной оценкой математического ожидания М(Х) (при любой функции распределения F(x) результатов наблюдений, для которой математическое ожидание существует). С помощью центральной предельной теоремы определяют асимптотические доверительные границы

(М(Х))_Н = , (М(Х))_В = .

где γ – доверительная вероятность,  - квантиль порядка  стандартного нормального распределения N(0;1) с нулевым математическим ожиданием и единичной дисперсией,  - выборочное среднее арифметическое, s – выборочное среднее квадратическое отклонение. Термин «асимптотические доверительные границы» означает, что вероятности

P{(M(X))_H < M(X)}, P{(M(X))_B > M(X)},

P{(M(X))_H < M(X) < (M(X))_B}

стремятся к ,  и γ соответственно при n → ∞, но, вообще говоря, не равны этим значениям при конечных n. Практически асимптотические доверительные границы дают достаточную точность при n порядка 10.

 Второй пример непараметрического оценивания – оценивание функции распределения. По теореме Гливенко эмпирическая функция распределения F_n(x) является состоятельной оценкой функции распределения F(x). Если F(x) – непрерывная функция, то на основе теоремы Колмогорова доверительные границы для функции распределения F(x) задают в виде

(F(x))_Н = max , (F(x))_B = min ,

где k(γ,n) – квантиль порядка γ распределения статистики Колмогорова при объеме выборки n (напомним, что распределение этой статистики не зависит от F(x)).

Правила определения оценок и доверительных границ в параметрическом случае строятся на основе параметрического семейства распределений F(x;θ). При обработке реальных данных возникает вопрос – соответствуют ли эти данные принятой вероятностной модели? Т.е. статистической гипотезе о том, что результаты наблюдений имеют функцию распределения из семейства {F(x;θ), θ Θ} при некотором θ = θ₀? Такие гипотезы называют гипотезами согласия, а критерии их проверки – критериями согласия.

Если истинное значение параметра θ = θ₀ известно, функция распределения F(x;θ₀) непрерывна, то для проверки гипотезы согласия часто применяют критерий Колмогорова, основанный на статистике

где F_n(x) – эмпирическая функция распределения.

 Если истинное значение параметра θ₀ неизвестно, например, при проверке гипотезы о нормальности распределения результатов наблюдения (т.е. при проверке принадлежности этого распределения к семейству нормальных распределений), то иногда используют статистику

Она отличается от статистики Колмогорова D_n тем, что вместо истинного значения параметра θ₀ подставлена его оценка θ*.

Распределение статистики D_n(θ*) сильно отличается от распределения статистики D_n. В качестве примера рассмотрим проверку нормальности, когда θ = (m, σ²), а θ* = ( , s²). Для этого случая квантили распределений статистик D_n и D_n(θ*) приведены в табл.1 (см., например, [15]). Таким образом, квантили отличаются примерно в 1,5 раза.

Таблица 1.

Квантили статистик D_n и D_n(θ*) при проверке нормальности

 При первичной обработке статистических данных важной задачей является исключение результатов наблюдений, полученных в результате грубых погрешностей и промахов. Например, при просмотре данных о весе (в килограммах) новорожденных детей наряду с числами 3,500, 2,750, 4,200 может встретиться число 35,00. Ясно, что это промах, и получено ошибочное число при ошибочной записи – запятая сдвинута на один знак, в результате результат наблюдения ошибочно увеличен в 10 раз.

 Статистические методы исключения резко выделяющихся результатов наблюдений основаны на предположении, что подобные результаты наблюдений имеют распределения, резко отличающиеся от изучаемых, а потому их следует исключить из выборки.

Простейшая вероятностная модель такова. При нулевой гипотезе результаты наблюдений рассматриваются как реализации независимых одинаково распределенных случайных величин X₁, X₂ , , X_n с функцией распределения F(x). При альтернативной гипотезе X₁, X₂ , , X_n-1 – такие же, как и при нулевой гипотезе, а X_n соответствует грубой погрешности и имеет функцию распределения G(x) = F(x – c), где с велико. Тогда с вероятностью, близкой к 1 (точнее, стремящейся к 1 при росте объема выборки),

X_n = max { X₁, X₂ , , X_n} = X_max ,

т.е. при описании данных в качестве возможной грубой ошибки следует рассматривать X_max . Критическая область имеет вид

Ψ = {x: x > d}.

Критическое значение d = d(α,n) выбирают в зависимости от уровня значимости α и объема выборки n из условия

P{X_max > d H₀} = α . (1)

Условие (1) эквивалентно при больших n и малых α следующему:

 (2)

Если функция распределения результатов наблюдений F(x) известна, то критическое значение d находят из соотношения (2). Если F(x) известна с точностью до параметров, например, известно, что F(x) – нормальная функция распределения, то также разработаны правила проверки рассматриваемой гипотезы [8].

Однако часто вид функции распределения результатов наблюдений известен не абсолютно точно и не с точностью до параметров, а лишь с некоторой погрешностью. Тогда соотношение (2) становится практически бесполезным, поскольку малая погрешность в определении F(x), как можно показать, приводит к большой погрешности при определении критического значения d из условия (2), а при фиксированном d уровень значимости критерия может существенно отличаться от номинального [2].

Поэтому в ситуации, когда о F(x) нет полной информации, однако известны математическое ожидание М(Х) и дисперсия σ² = D(X) результатов наблюдений X₁, X₂ , , X_n, можно использовать непараметрические правила отбраковки, основанные на неравенстве Чебышёва. С помощью этого неравенства найдем критическое значение d = d(α,n) такое, что

Так как

то соотношение (3) будет выполнено, если

 (4)

По неравенству Чебышёва

 (5)

поэтому для того, чтобы (4) было выполнено, достаточно приравнять правые части формул (4) и (5), т.е. определить d из условия

 (6)

Правило отбраковки, основанное на критическом значении d, вычисленном по формуле (6), использует минимальную информацию о функции распределения F(x) и поэтому исключает лишь результаты наблюдений, весьма далеко отстоящие от основной массы. Другими словами, значение d₁, заданное соотношением (1), обычно много меньше, чем значение d₂, заданное соотношением (6).

 Многомерный статистический анализ. Перейдем к многомерному статистическому анализу. Его применяют при решении следующих задач:

 • исследование зависимости между признаками;

• классификация объектов или признаков, заданных векторами;

• снижение размерности пространства признаков.

При этом результат наблюдений – вектор значений фиксированного числа количественных и иногда качественных признаков, измеренных у объекта. Напомним, что количественный признак – признак наблюдаемой единицы, который можно непосредственно выразить числом и единицей измерения. Количественный признак противопоставляется качественному - признаку наблюдаемой единицы, определяемому отнесением к одной из двух или более условных категорий (если имеется ровно две категории, то признак называется альтернативным). Статистический анализ качественных признаков – часть статистики объектов нечисловой природы. Количественные признаки делятся на признаки, измеренные в шкалах интервалов, отношений, разностей, абсолютной.

А качественные – на признаки, измеренные в шкале наименований и порядковой шкале. Методы обработки данных должны быть согласованы со шкалами, в которых измерены рассматриваемые признаки (см. раздел 2.1 о теории измерений).

 Целями исследования зависимости между признаками являются доказательство наличия связи между признаками и изучение этой связи. Для доказательства наличия связи между двумя случайными величинами Х и У применяют корреляционный анализ. Если совместное распределение Х и У является нормальным, то статистические выводы основывают на выборочном коэффициенте линейной корреляции, в остальных случаях используют коэффициенты ранговой корреляции Кендалла и Спирмена, а для качественных признаков – критерий хи-квадрат.

 Регрессионный анализ применяют для изучения функциональной зависимости количественного признака У от количественных признаков x(1), x(2), … , x(k). Эту зависимость называют регрессионной или, кратко, регрессией. Простейшая вероятностная модель регрессионного анализа (в случае k = 1) использует в качестве исходной информации набор пар результатов наблюдений (x_i, y_i), i = 1, 2, … , n, и имеет вид

y_i = ax_i + b + ε_i, i = 1, 2, … , n,

где ε_i – ошибки наблюдений. Иногда предполагают, что ε_i – независимые случайные величины с одним и тем же нормальным распределением N(0, σ²). Поскольку распределение ошибок наблюдения обычно отлично от нормального, то целесообразно рассматривать регрессионную модель в непараметрической постановке [2], т.е. при произвольном распределении ε_i.

 Основная задача регрессионного анализа состоит в оценке неизвестных параметров а и b, задающих линейную зависимость y от x. Для решения этой задачи применяют разработанный еще К.Гауссом в 1794 г. метод наименьших квадратов, т.е. находят оценки неизвестных параметров моделиa и b из условия минимизации суммы квадратов

по переменным а и b.

 Теория регрессионного анализа описана и расчетные формулы даны в специальной литературе [2, 16, 17]. В этой теории разработаны методы точечного и интервального оценивания параметров, задающих функциональную зависимость, а также непараметрические методы оценивания этой зависимости, методы проверки различных гипотез, связанных с регрессионными зависимостями. Выбор планов эксперимента, т.е. точек x_i, в которых будут проводиться эксперименты по наблюдению y_i – предмет теории планирования эксперимента [18]. 

 Дисперсионный анализ применяют для изучения влияния качественных признаков на количественную переменную. Например, пусть имеются k выборок результатов измерений количественного показателя качества единиц продукции, выпущенных на k станках, т.е. набор чисел (x₁(j), x₂(j), … , x_n(j)), где j – номер станка, j = 1, 2, …, k, а n – объем выборки. В распространенной постановке дисперсионного анализа предполагают, что результаты измерений независимы и в каждой выборке имеют нормальное распределение N(m(j), σ²) с одной и той же дисперсией. Хорошо разработаны и непараметрические постановки [19].

 Проверка однородности качества продукции, т.е. отсутствия влияния номера станка на качество продукции, сводится к проверке гипотезы

H₀: m(1) = m(2) = … = m(k).

В дисперсионном анализе разработаны методы проверки подобных гипотез. Теория дисперсионного анализа и расчетные формулы рассмотрены в специальной литературе [20].

 Гипотезу Н₀ проверяют против альтернативной гипотезы Н₁, согласно которой хотя бы одно из указанных равенств не выполнено. Проверка этой гипотезы основана на следующем «разложении дисперсий», указанном Р.А.Фишером:

 (7)

где s² – выборочная дисперсия в объединенной выборке, т.е.

Далее, s²(j) – выборочная дисперсия в j-ой группе,

Таким образом, первое слагаемое в правой части формулы (7) отражает внутригрупповую дисперсию. Наконец,  - межгрупповая дисперсия,

 Область прикладной статистики, связанную с разложениями дисперсии типа формулы (7), называют дисперсионным анализом. В качестве примера задачи дисперсионного анализа рассмотрим проверку приведенной выше гипотезы Н₀ в предположении, что результаты измерений независимы и в каждой выборке имеют нормальное распределение N(m(j), σ²) с одной и той же дисперсией. При справедливости Н₀ первое слагаемое в правой части формулы (7), деленное на σ², имеет распределение хи-квадрат с k(n-1) степенями свободы, а второе слагаемое, деленное на σ², также имеет распределение хи-квадрат, но с (k-1) степенями свободы, причем первое и второе слагаемые независимы как случайные величины. Поэтому случайная величина

имеет распределение Фишера с (k-1) степенями свободы числителя и k(n-1) степенями свободы знаменателя. Гипотеза Н₀ принимается, если F < F_1-α, и отвергается в противном случае, где F_1-α – квантиль порядка 1-α распределения Фишера с указанными числами степеней свободы. Такой выбор критической области определяется тем, что при Н₁ величина F безгранично увеличивается при росте объема выборок n. Значения F_1-α берут из соответствующих таблиц [8].

Разработаны непараметрические методы решения классических задач дисперсионного анализа [19], в частности, проверки гипотезы Н₀.

Следующий тип задач многомерного статистического анализа – задачи классификации. Они согласно [2, 20] делятся на три принципиально различных вида – дискриминантный анализ, кластер-анализ, задачи группировки.

Задача дискриминантного анализа состоит в нахождении правила отнесения наблюдаемого объекта к одному из ранее описанных классов. При этом объекты описывают в математической модели с помощью векторов, координаты которых – результаты наблюдения ряда признаков у каждого объекта. Классы описывают либо непосредственно в математических терминах, либо с помощью обучающих выборок. Обучающая выборка – это выборка, для каждого элемента которой указано, к какому классу он относится.

Рассмотрим пример применения дискриминантного анализа для принятия решений в технической диагностике. Пусть по результатам измерения ряда параметров продукции необходимо установить наличие или отсутствие дефектов. В этом случае для элементов обучающей выборки указаны дефекты, обнаруженные в ходе дополнительного исследования, например, проведенного после определенного периода эксплуатации. Дискриминантный анализ позволяет сократить объем контроля, а также предсказать будущее поведение продукции. Дискриминантный анализ сходен с регрессионным – первый позволяет предсказывать значение качественного признака, а второй – количественного. В статистике объектов нечисловой природы разработана математическая схема, частными случаями которой являются регрессионный и дискриминантный анализы [21].

Кластерный анализ применяют, когда по статистическим данным необходимо разделить элементы выборки на группы. Причем два элемента группы из одной и той же группы должны быть «близкими» по совокупности значений измеренных у них признаков, а два элемента из разных групп должны быть «далекими» в том же смысле. В отличие от дискриминантного анализа в кластер-анализе классы не заданы, а формируются в процессе обработки статистических данных. Например, кластер-анализ может быть применен для разбиения совокупности марок стали (или марок холодильников) на группы сходных между собой.

Другой вид кластер-анализа – разбиение признаков на группы близких между собой. Показателем близости признаков может служить выборочный коэффициент корреляции. Цель кластер-анализа признаков может состоять в уменьшении числа контролируемых параметров, что позволяет существенно сократить затраты на контроль. Для этого из группы тесно связанных между собой признаков (у которых коэффициент корреляции близок к 1 – своему максимальному значению) измеряют значение одного, а значения остальных рассчитывают с помощью регрессионного анализа.

Задачи группировки решают тогда, когда классы заранее не заданы и не обязаны быть «далекими» друг от друга. Примером является группировка студентов по учебным группам. В технике решением задачи группировки часто является параметрический ряд – возможные типоразмеры группируются согласно элементам параметрического ряда. В литературе, нормативно-технических и инструктивно-методических документах по прикладной статистике также иногда используется группировка результатов наблюдений (например, при построении гистограмм).

Задачи классификации решают не только в многомерном статистическом анализе, но и тогда, когда результатами наблюдений являются числа, функции или объекты нечисловой природы. Так, многие алгоритмы кластер-анализа используют только расстояния между объектами. Поэтому их можно применять и для классификации объектов нечисловой природы, лишь бы были заданы расстояния между ними. Простейшая задача классификации такова: даны две независимые выборки, требуется определить, представляют они два класса или один. В одномерной статистике эта задача сводится к проверке гипотезы однородности [2].

Третий раздел многомерного статистического анализа – задачи снижения размерности (сжатия информации). Цель их решения состоит в определении набора производных показателей, полученных преобразованием исходных признаков, такого, что число производных показателей значительно меньше числа исходных признаков, но они содержат возможно большую часть информации, имеющейся в исходных статистических данных. Задачи снижения размерности решают с помощью методов многомерного шкалирования, главных компонент, факторного анализа и др. Например, в простейшей модели многомерного шкалирования исходные данные – попарные расстояния  между k объектами, а цель расчетов состоит в представлении объектов точками на плоскости. Это дает возможность в буквальном смысле слова увидеть, как объекты соотносятся между собой. Для достижения этой цели необходимо каждому объекту поставить в соответствие точку на плоскости так, чтобы попарные расстояния s_ij между точками, соответствующими объектам с номерами i и j, возможно точнее воспроизводили расстояния ρ_ij между этими объектами. Согласно основной идее метода наименьших квадратов находят точки на плоскости так, чтобы величина

достигала своего наименьшего значения. Есть и многие другие постановки задач снижения размерности и визуализации данных.

 Статистика случайных процессов и временных рядов. Методы статистики случайных процессов и временных рядов применяют для постановки и решения, в частности, следующих задач:

 • предсказание будущего развития случайного процесса или временного ряда;

• управление случайным процессом (временным рядом) с целью достижения поставленных целей, например, заданных значений контролируемых параметров;

• построение вероятностной модели реального процесса, обычно длящегося во времени, и изучение свойств этой модели.

 Пример 1. При внедрении статистического регулирования технологического процесса необходимо проверить, что в налаженном состоянии математическое ожидание контролируемого параметра не меняется со временем. Если подобное изменение будет обнаружено, то необходимо установить подналадочное устройство.

 Пример 2. Следящие системы, например, входящие в состав автоматизированной системы управления технологическим процессом, должны выделять полезный сигнал на фоне шумов. Это – задача оценивания (полезного сигнала), в то время как в примере 1 речь шла о задаче проверки гипотезы.

 Методы статистики случайных процессов и временных рядов описаны в литературе [2,20].

 Статистика объектов нечисловой природы. Методы статистики объектов нечисловой природы применяют всегда, когда результаты наблюдений являются объектами нечисловой природы. Например, сообщениями о годности или дефектности единиц продукции. Информацией о сортности единиц продукции. Разбиениями единиц продукции на группы соответственно значения контролируемых параметров. Упорядочениями единиц продукции по качеству или инвестиционных проектов по предпочтительности. Фотографиями поверхности изделия, пораженной коррозией, и т.д. Итак, объекты нечисловой природы – это измерения по качественному признаку, множества, бинарные отношения (разбиения, упорядочения и др.) и многие другие математические объекты [2]. Они используются в различных вероятностно-статистических методах принятия решений. В частности, в задачах управления качеством продукции, а также, например, в медицине и социологии, как для описания результатов приборных измерений, так и для анализа экспертных оценок.

 Для описания данных, являющихся объектами нечисловой природы, применяют, в частности, таблицы сопряженности, а в качестве средних величин – решения оптимизационных задач [2]. В качестве выборочных средних для измерений в порядковой шкале используют медиану и моду, а в шкале наименований – только моду. О методах классификации нечисловых данных говорилось выше.

 Для решения параметрических задач оценивания используют оптимизационный подход, метод одношаговых оценок, метод максимального правдоподобия, метод устойчивых оценок. Для решения непараметрических задач оценивания наряду с оптимизационными подходами к оцениванию характеристик используют непараметрические оценки распределения случайного элемента, плотности распределения, функции, выражающей зависимость [2].

 В качестве примера методов проверки статистических гипотез для объектов нечисловой природы рассмотрим критерий «хи-квадрат» (обозначают χ²), разработанный К.Пирсоном для проверки гипотезы однородности (другими словами, совпадения) распределений, соответствующих двум независимым выборкам.

 Рассматриваются две выборки объемов n₁ и n₂, состоящие из результатов наблюдений качественного признака, имеющего k градаций. Пусть m_1j и m_2j – количества элементов первой и второй выборок соответственно, для которых наблюдается j–я градация, а p_1j и p_2j – вероятности того, что эта градация будет принята, для элементов первой и второй выборок, j = 1, 2, …, k.

 Для проверки гипотезы однородности распределений, соответствующих двум независимым выборкам,

H₀: p_1j = p_2j, j = 1, 2, …, k,

применяют критерий χ² (хи-квадрат) со статистикой

Установлено [9, 11], что статистика Х² при больших объемах выборок n₁ и n₂ имеет асимптотическое распределение хи-квадрат с (k – 1) степенью свободы.

Таблица 1

Распределения плавок стали по процентному содержанию серы

 Пример 3. В табл.1 приведены данные о содержании серы в углеродистой стали, выплавляемой двумя металлургическими заводами. Проверим, можно ли считать распределения примеси серы в плавках стали этих двух заводов одинаковыми.

 Расчет по данным табл.1 дает Х² = 3,39. Квантиль порядка 0,95 распределения хи-квадрат с k – 1 = 3 степенями свободы равен  а потому гипотезу о совпадении функций распределения содержания серы в плавках двух заводов нельзя отклонить, т.е. ее следует принять (на уровне значимости α = 0,05).

 Методы статистики объектов нечисловой природы рассмотрены в [2].

 Выше дано краткое описание содержания прикладной статистики на современном этапе. Подробное изложение конкретных методов содержится в специальной литературе.

 Некоторые постановки задач прикладной статистики, используемые в вероятностно-статистических методах принятия решений. Чтобы дать представление о богатом содержании теории рассматриваемых методов, приведем краткий перечень основных типов постановок задач в соответствии с описанной выше классификацией областей прикладной статистики.

1. Одномерная статистика.

1.1. Описание материала

1.1.1. Расчет выборочных характеристик распределения.

1.1.2. Построение гистограмм и полигонов часто.

1.1.3. Приближение эмпирических распределений с помощью распределений из системы Пирсона и других систем…

1.2. Оценивание.

1.2.1. Параметрическое оценивание.

1.2.1.1. Правила определения оценок и доверительных границ для параметров устойчивого распределения.

1.2.1.2. Правила определения оценок и доверительных границ для параметров логистического распределения.

1.2.1.3. Правила определения оценок и доверительных границ для параметров экспоненциального распределения и смеси экспоненциальных распределений… (и так далее для различных семейств распределений).

1.2.2. Непараметрическое оценивание.

1.2.2.1. Непараметрическое точечное и доверительное оценивание основных характеристик распределения – математического ожидания, дисперсии, среднего квадратического отклонения, коэффициента вариации, квантилей, прежде всего медианы.

1.2.2.2. Непараметрические оценки плотности и функции распределения.

1.2.2.3. Непараметрическое оценивание параметра сдвига…

1.3. Проверка гипотез.

1.3.1. Параметрические задачи проверки гипотез.

1.3.1.1. Проверка равенства математических ожиданий для двух нормальных совокупностей.

1.3.1.2. Проверка равенства дисперсий для двух нормальных совокупностей.

1.3.1.3. Проверка равенства коэффициентов вариации для двух нормальных совокупностей.

1.3.1.4. Проверка равенства математических ожиданий и дисперсий для двух нормальных совокупностей.

1.3.1.5. Проверка равенства математического ожидания нормального распределения определенному значению.

1.3.1.6. Проверка равенства дисперсии нормального распределения определенному значению…

1.3.1.7. Проверка равенства параметров двух экспоненциальных совокупностей… (и так далее – проверка утверждений о параметрах для различных семейств распределений).

1.3.2. Непараметрические задачи проверки гипотез.

1.3.2.1. Непараметрическая проверка равенства математических ожиданий для двух совокупностей.

1.3.2.2. Непараметрическая проверка равенства дисперсий для двух совокупностей.

1.3.2.3. Непараметрическая проверка равенства коэффициентов вариации для двух совокупностей.

1.3.2.4. Непараметрическая проверка равенства математических ожиданий и дисперсий для двух совокупностей.

1.3.2.5. Непараметрическая проверка равенства математического ожидания определенному значению.

1.3.2.6. Непараметрическая проверка равенства дисперсии определенному значению…

1.3.2.7. Проверка гипотезы согласия с равномерным распределением по критерию Колмогорова.

1.3.2.8. Проверка гипотезы согласия с равномерным распределением по критерию омега-квадрат (Крамера-Мизеса-Смирнова).

1.3.2.9. Проверка гипотезы согласия с равномерным распределением по критерию Смирнова.

1.3.2.10. Проверка гипотезы согласия с нормальным семейством распределений по критерию типа Колмогорова при известной дисперсии.

1.3.2.11. Проверка гипотезы согласия с нормальным семейством распределений по критерию типа Колмогорова при известном математическом ожидании.

1.3.2.12. Проверка гипотезы согласия с нормальным семейством распределений по критерию типа Колмогорова (оба параметра неизвестны).

1.3.2.13. Проверка гипотезы согласия с нормальным семейством распределений по критерию типа омега-квадрат при известной дисперсии.

1.3.2.14. Проверка гипотезы согласия с нормальным семейством распределений по критерию типа омега-квадрат при известном математическом ожидании.

1.3.2.15. Проверка гипотезы согласия с нормальным семейством распределений по критерию типа омега-квадрат (оба параметра неизвестны).

1.3.2.16. Проверка гипотезы согласия с экспоненциальным семейством распределений по критерию типа омега-квадрат… ( и так далее для различных семейств распределений, тех или иных предположениях о параметрах, всевозможных критериев). 

1.3.2.17. Проверка гипотезы однородности двух выборок методом Смирнова.

1.3.2.18. Проверка гипотезы однородности двух выборок методом омега-квадрат.

1.3.2.19. Проверка гипотезы однородности двух выборок с помощью критерия Вилкоксона.

1.3.2.20. Проверка гипотезы однородности двух выборок по критерию Ван-дер-Вардена.

1.3.2.21. Проверка гипотезы симметрии функции распределения относительно 0 методом Смирнова.

1.3.2.22. Проверка гипотезы симметрии функции распределения относительно 0 с помощью критерия типа омега-квадрат (Орлова).

1.3.2.23. Проверка гипотезы независимости элементов выборки.

1.3.2.24. Проверка гипотезы одинаковой распределенности элементов выборки…(и т.д.).

2. Многомерный статистический анализ.

2.1. Описание материала.

2.1.1. Расчет выборочных характеристик (вектора средних, ковариационной и корреляционной матриц и др.).

2.1.2. Таблицы сопряженности.

2.1.3. Детерминированные методы приближения функциональной зависимости.

2.1.3.1. Метод наименьших квадратов.

2.1.3.2. Метод наименьших модулей

2.1.3.3. Сплайны и др.

2.1.4. Методы снижения размерности.

2.1.4.1. Алгоритмы факторного анализа.

2.1.4.2. Алгоритмы метода главных компонент

2.1.4.3. Алгоритмы многомерного метрического шкалирования.

2.1.4.4. Алгоритмы многомерного неметрического шкалирования.

2.1.4.5. Методы оптимального проецирования и др.

2.1.5. Методы классификации.

2.1.5.1. Методы кластер-анализа – иерархические процедуры.

2.1.5.2. Методы кластер-анализа – оптимизационный подход.

2.1.5.3. Методы кластер-анализа – итерационные процедуры…

2.1.5.4. Методы группировки…

2.2. Оценивание.

2.2.1. Параметрическое оценивание.

2.2.1.1. Оценивание параметров многомерного нормального распределения.

2.2.1.2. Оценивание параметров в нормальной модели линейной регрессии.

2.2.1.3. Методы расщепления смесей.

2.2.1.4. Оценивание компонент дисперсии в дисперсионном анализе (в нормальной модели).

2.2.1.5. Оценивание размерности и структуры модели в регрессионном анализе (в нормальной модели).

2.2.1.6. Оценивание в дискриминантном анализе (в нормальной модели).

2.2.1.7. Оценивание в методах снижения размерности (в нормальной модели).

2.2.1.8. Нелинейная регрессия.

2.2.1.9. Методы планирования эксперимента.

2.2.2. Непараметрическое оценивание.

2.2.2.1. Непараметрические оценки многомерной плотности.

2.2.2.2. Непараметрическая регрессия (с погрешностями наблюдений произвольного вида).

2.2.2.3. Непараметрическая регрессия (на основе непараметрических оценок многомерной плотности).

2.2.2.4. Монотонная регрессия.

2.2.2.5. Непараметрический дискриминантный анализ.

2.2.2.6. Непараметрический дисперсионный анализ…

2.3. Проверка гипотез.

2.3.1. Параметрические задачи проверки гипотез.

2.3.1.1. Корреляционный анализ (нормальная модель).

2.3.1.2. Проверка гипотез об отличии коэффициентов при предикторах от 0 в линейной регрессии при справедливости нормальной модели.

2.3.1.3. Проверка гипотезы о равенстве математических ожиданий нормальных совокупностей (дисперсионный анализ).

2.3.1.4. Проверка гипотезы о совпадении двух линий регрессии (нормальная модель)…(и т.д.)

2.3.2. Непараметрические задачи проверки гипотез.

2.3.2.1. Непараметрический корреляционный анализ.

2.3.2.2. Проверка гипотез об отличии коэффициентов при предикторах от 0 в линейной регрессии (непараметрическая постановка).

2.3.2.3. Проверка гипотез в непараметрическом дисперсионном анализе.

2.3.2.4. Проверка гипотезы о совпадении двух линий регрессии (непараметрическая постановка)…(и т.д.)

 Здесь остановимся, поскольку продолжение предполагало бы знакомство со многими достаточно сложными методами, о которых нет упоминаний в этой книге. Приведенный выше перечень ряда основных типов постановок задач, используемых в вероятностно-статистических методах принятия решений, дает первоначальное представление об объеме арсенала разработанных к настоящему времени интеллектуальных инструментов в рассматриваемой области.

Литература

1. Вероятность и математическая статистика: Энциклопедия/Гл. ред. Ю.В.Прохоров. – М.: Большая Российская энциклопедия, 1999. – 910с.

2. Орлов А.И. Эконометрика. – М.: Экзамен, 2002. - 576 с.

3. Рекомендации. Прикладная статистика. Методы обработки данных. Основные требования и характеристики / Орлов А.И., Фомин В.Н. и др. - М.: ВНИИСтандартизации, 1987. 62 с.

4. Колмогоров А.Н. Основные понятия теории вероятностей. – М.-Л.: ОНТИ, 1936. 80 с.

5. Колмогоров А.Н. Теория информации и теория алгоритмов. – М.: Наука, 1987. 304 с.

6. Гнеденко Б.В. Курс теории вероятностей: Учебник. 7-е изд., исправл. - М.: Эдиториал УРСС, 2001. 320 с.

7. Орлов А.И. Устойчивость в социально-экономических моделях. – М.: Наука, 1979. 296 с.

8. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1965 (1-е изд.), 1968 (2-е изд.), 1983 (3-е изд.).

9. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. – М.: Наука, 1969. 512 с.

10. Колмогоров А.Н. О логарифмически нормальном законе распределения размеров частиц при дроблении / Доклады АН СССР. 1941. Т.31. С.99-101.

11. Крамер Г. Математические методы статистики. – М.: Мир, 1975. 648 с.

12. Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. (Основные понятия. Предельные теоремы. Случайные процессы.) – М.: Наука, 1973. 496 с.

13. Камень Ю.Э., Камень Я.Э., Орлов А.И. Реальные и номинальные уровни значимости в задачах проверки статистических гипотез. - Журнал «Заводская лаборатория». 1986. Т.52. No.12. С.55-57.

14. Орлов А.И. О нецелесообразности использования итеративных процедур нахождения оценок максимального правдоподобия. – Журнал «Заводская лаборатория», 1986, т.52, No.5, с.67-69.

15. Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат. – Журнал «Заводская лаборатория».1985. Т.51. No.1. С.60-62.

16. Кендалл М.Дж., Стъюарт А. Статистические выводы и связи. - М.: Наука, 1973. – 900 с.

17. Себер Дж. Линейный регрессионный анализ. - М.: Мир, 1980. - 456 с.

18. Математическая теория планирования эксперимента / Под ред. С.М.Ермакова. - М.: Наука, 1983. – 392 с.

19. Холлендер М., Вульф Д. Непараметрические методы статистики. – М.: Финансы и статистика, 1983. - 518 с.

20. Кендалл М.Дж., Стьюарт А. Многомерный статистический анализ и временные ряды. - М.: Наука, 1976. – 736 с.

21. Орлов А.И. Некоторые неклассические постановки в регрессионном анализе и теории классификации. - В сб.: Программно-алгоритмическое обеспечение анализа данных в медико-биологических исследованиях. - М.: Наука, 1987. с.27-40.

Контрольные вопросы и задачи

1. Расскажите о понятиях случайного события и его вероятности.

2. Почему закон больших чисел и центральная предельная теорема занимают центральное место в вероятностно-статистических методах принятия решений?

3. Чем многомерный статистический анализ отличается от статистики объектов нечисловой природы?

4. Имеются три одинаковые с виду ящика. В первом а белых шаров и b черных; во втором c белых и d черных; в третьем только белые шары. Некто подходит наугад к одному из ящиков и вынимает из нее один шар. Найдите вероятность того, что этот шар белый.

5. Пассажир может воспользоваться трамваями двух маршрутов, следующих с интервалами Т₁ и Т₂ соответственно. Пассажир может прийти на остановку в некоторый произвольный момент времени. Какой может быть вероятность того, что пассажир, пришедший на остановку, будет ждать не дольше t, где 0<t<min(T₁,T₂)?

6. Два стрелка, независимо один от другого, делают по два выстрела (каждый по своей мишени). Вероятность попадания в мишень при одном выстреле для первого стрелка p₁, для второго p₂.Выигравшим соревнование считается тот стрелок, в мишени которого будет больше пробоин. Найти вероятность того, что выиграет первый стрелок.

7. Полная колода карт(52 листа) делится наугад на две равные пачки по 26 листов. Найти вероятности следующих событий:

 A - в каждой из пачек окажется по два туза;

 B - в одной из пачек не будет ни одного туза, а в другой все четыре;

 C - в одной из пачек будет один туз, а в другой три.

8. Случайная величина X принимает значения 0 и 1, а случайная величина Y - значения (-1), 0 и 1. Вероятности P(X=i, Y=j) задаются таблицей:

Найдите распределение случайной величины Z = XY, ее математическое ожидание и дисперсию.

9. В условиях задачи 8 найдите распределение случайной величины W = X/(Y+3), ее математическое ожидание и дисперсию.

10. Даны независимые случайные величины X и Y такие, что М(X) = 1 , D(X) = 3, М(Y) = -1, D(Y) = 2. Найдите М(aX + bY) и D(aX + bY), где a= 3 , b= -2.

Темы докладов, рефератов, исследовательских работ

1. Описание данных с помощью гистограмм и непараметрических оценок плотности.

2. Сравнительный анализ методов оценивания параметров и характеристик.

3. Преимущества одношаговых оценок по сравнению с оценками метода максимального правдоподобия.

4. Непараметрический регрессионный анализ.

5. Аксиоматическое введение метрик и их использование в статистике объектов нечисловой природы.

6. Законы больших чисел в пространствах произвольной природы, в том числе в дискретных пространствах.

7. Оптимизационные постановки в вероятностно-статистических задачах принятия решений.