 Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Прикладная статистика: Асимптотика решений экстремальных статистических задачЧасть 2. Основные проблемы прикладной статистики 2.2. Оценивание 2.2.3. Асимптотика решений экстремальных статистических задач Если проанализировать приведенные выше в подразделе 2.1.5 постановки и результаты, касающиеся эмпирических и теоретических средних и законов больших чисел, то становится очевидной возможность их обобщения. Так, доказательства теорем практически не меняются, если считать, что функция f(x,y) определена на декартовом произведении бикомпактных пространств X и Y, а не на X2. Тогда можно считать, что элементы выборки лежат в Х, а Y - пространство параметров, подлежащих оценке. Обобщения законов больших чисел. Пусть, например, выборка х1 = х1(ω), х2 = х2(ω), … , хn = хn(ω) взята из распределения с плотностью p(x,y), где у – неизвестный параметр. Если положить f(x,y) = - ln p(x,y), то задача нахождения эмпирического среднего
переходит в задачу оценивания неизвестного параметра y методом максимального правдоподобия
Соответственно законы больших чисел переходят в утверждения о состоятельности этих оценок в случае пространств X и Y общего вида. При такой интерпретации функция f(x,y) уже не является расстоянием или показателем различия. Однако для доказательства сходимости оценок к соответствующим значениям параметров это и не требуется. Достаточно непрерывности этой функции на декартовом произведении бикомпактных пространств X и Y. В случае функции f(x,y) общего вида можно говорить об определении в пространствах произвольной природы оценок минимального контраста и их состоятельности. При этом при каждом конкретном значении параметра у справедливо предельное соотношение
где f – функция контраста. Тогда состоятельность оценок минимального контраста вытекает из справедливости предельного перехода
Частными случаями оценок минимального контраста являются, устойчивые (робастные) оценки Тьюки-Хубера (см. ниже), а также оценки параметров в задачах аппроксимации (параметрической регрессии) в пространствах произвольной природы. Можно пойти и дальше в обобщении законов больших чисел. Пусть известно, что при каждом конкретном y при безграничном росте n имеет быть сходимость по вероятности fn( где fn(ω, y) – последовательность случайных функций на пространстве Y, а f(y) – некоторая функция на У. В каких случаях и в каком смысле имеет место сходимость Argmin {fn( Другими словами, когда из поточечной сходимости функций вытекает сходимость точек минимума? Причем здесь можно под n понимать натуральное число. А можно рассматривать сходимость по направленному множеству (подраздел 1.4.3), или же, что практически то же самое – «сходимость по фильтру» в смысле Картана и Бурбаки [19, с.118]. В частности, можно описывать ситуацию вектором, координаты которого - объемы нескольких выборок, и все они безгранично растут. В классической математической статистике такие постановки рассматривать не любят. Поскольку, как уже отмечалось, основные задачи прикладной статистики можно представить в виде оптимизационных задач, то ответ на поставленный вопрос о сходимости точек минимума дает возможность единообразного подхода к изучению асимптотики решений разнообразных экстремальных статистических задач. Одна из возможных формулировок, основанная на бикомпактности пространств Х и У и нацеленная на изучение оценок минимального контраста, дана и обоснована выше. Другой подход развит в работе [20]. Он основан на использовании понятий асимптотической равномерной разбиваемости и координатной асимптотической равномерной разбиваемости пространств. С помощью указанных подходов удается стандартным образом обосновывать состоятельность оценок характеристик и параметров в основных задачах прикладной статистики. Рассматриваемую тематику можно развивать дальше, в частности, рассматривать аналоги законов больших чисел в случае пространств, не являющихся бикомпактными, а также изучать скорость сходимости Argmin{fn(x( Приведем примеры применения результатов о предельном поведении точек минимума. Задача аппроксимации зависимости (параметрической регрессии). Пусть X и Y – некоторые пространства. Пусть имеются статистические данные - n пар (xk, yk), где xk
Часто, но не всегда, все fk совпадают. В классической постановке, когда Х = Rk, У = R1, функции fk различны при неравноточных наблюдениях, например, когда число опытов меняется от одной точки х проведения опытов к другой. Если fk(y1,y2) = f(y1,y2) = (y1- y2)2, то получаем общую постановку метода наименьших квадратов (см. подробности в главе 3.2):
В рамках детерминированного анализа данных остается единственный теоретический вопрос – о существовании θn. Если все участвующие в формулировке задачи (1) функции непрерывны, а минимум берется по бикомпакту, то θn существует. Есть и иные условия существования θn [20-22]. При появлении нового наблюдения х в соответствии с методологией восстановления зависимости рекомендуется выбирать оценку соответствующего у по правилу у* = g(x, θn). Обосновать такую рекомендацию в рамках детерминированного анализа данных невозможно. Это можно сделать только в вероятностной теории, равно как и изучить асимптотическое поведение θn, доказать состоятельность этой оценки. Кпк и в классическом случае, вероятностную теорию целесообразно строить для трех различных постановок. 1. Переменная х – детерминированная (например, время), переменная у – случайная, ее распределение зависит от х. 2. Совокупность (xk, yk), k = 1, 2, …, n, – выборка из распределения случайного элемента со значениями в ХЧУ. 3. Имеется детерминированный набор пар (xk0, yk0), k = 1, 2, …, n, результат наблюдения (xk, yk) является случайным элементом, распределение которого зависит от (xk0, yk0). Это – постановка конфлюэнтного анализа. Во всех трех случаях
однако случайность входит в правую часть по-разному в зависимости от постановки, от которой зависит и определение предельной функции f(θ). Проще всего выглядит f(θ) в случае второй постановки при fk ≡ f: f(θ) = Mf(g(x1,θ),y). В случае первой постановки
в предположении существования указанного предела. Ситуация усложняется для третьей постановки:
Во всех трех случаях на основе общих результатов о поведении решений экстремальных статистических задач можно изучить [20-22] асимптотику оценок θn. При выполнении соответствующих внутриматематических условий регулярности оценки оказываются состоятельными, т.е. удается восстановить зависимость. Аппроксимация и регрессия. Соотношение (1) дает решение задачи аппроксимации. Поясним, как эта задача соотносится с нахождением регрессии. Согласно [23] для случайной величины (ξ, η) со значениями в ХЧУ регрессией η на ξ относительно меры близости f естественно назвать решение задачи Mf(g(ξ), η) → где f: YЧY → R1, g: X → Y, минимум берется по множеству всех измеримых функций. Можно исходить и из другого определения. Для каждого х
Оказывается, при обычных предположениях измеримости решение задачи (2) совпадает с Если заранее известно, что условное математическое ожидание Пусть ν1 – мера в Х, ν2 – мера в У, а их прямое произведение ν = ν1Чν2 – мера в ХЧУ. Пусть g(x,y) – плотность случайного элемента (ξ,η) по мере ν. Тогда условная плотность g(yx) распределения η при условии ξ=х имеет вид
(в предположении, что интеграл в знаменателе отличен от 0). Следовательно,
а потому
Заменяя g(x,y) в (3) непараметрической оценкой плотности gn(x,y), получаем оценку условной плотности
Если gn(x,y) – состоятельная оценка g(x,y), то числитель (4) сходится к числителю (3). Сходимость знаменателя (4) к знаменателю (3) обосновывается с помощью предельной теории статистик интегрального типа (см главу 2.3). В итоге получаем утверждение о состоятельности непараметрической оценки (4) условной плотности (3). Непараметрическая оценка регрессии ищется как
Состоятельность этой оценки следует из приведенных выше общих результатов об асимптотическом поведении решений экстремальных статистических задач. Применение к методу главных компонент. Исходные данные – набор векторов ξ1, ξ2, … , ξn, лежащих в евклидовом пространстве Rk размерности k. Цель состоит в снижении размерности, т.е. в уменьшении числа рассматриваемых показателей. Для этого берут всевозможные линейные ортогональные нормированные центрированные комбинации исходных показателей, получают k новых показателей, из них берут первые m, где m < k (подробности см. в главе 3.2). Матрицу преобразования С выбирают так, чтобы максимизировать информационный функционал
где x(i), i = 1, 2, … , k, - исходные показатели; исходные данные имеют вид ξj = (xj(1), xj(2), … , xj(k)), j = 1, 2, … , n; при этом z(α), α = 1, 2, … , m, - комбинации исходных показателей, полученные с помощью матрицы С. Наконец, s2(z(α)), α = 1, 2, … , m, s2(x(i)), i = 1, 2, … , k, - выборочные дисперсии переменных, указанных в скобках. Укажем подробнее, как новые показатели (главные компоненты) z(α) строятся по исходным показателям x(i) с помощью матрицы С:
где
Матрица C = cαβ порядка mЧk такова, что
(нормированность),
(ортогональность). Решением основной задачи метода главных компонент является
где минимизируемая функция определена формулой (5), а минимизация проводится по всем матрицам С, удовлетворяющим условиям (6) и (7). Вычисление матрицы Сn – задача детерминированного анализа данных. Однако, как и в иных случаях, например, для медианы Кемени, возникает вопрос об асимптотическом поведении Сn. Является ли решение основной задачи метода главных компонент устойчивым, т.е. существует ли предел Сn при n → ∞? Чему равен этот предел? Ответ, как обычно, может быть дан только в вероятностной теории. Пусть ξ1, ξ2, … , ξn - независимые одинаково распределенные случайные вектора. Положим
где матрица C = cαβ удовлетворяет условиям (6) и (7). Введем функцию от матрицы
Легко видеть, что при n → ∞ и любом С
Рассмотрим решение предельной экстремальной задачи
Естественно ожидать, что
Действительно, это соотношение вытекает из приведенных выше общих результатов об асимптотическом поведении решений экстремальных статистических задач. Таким образом, теория, развитая для пространств произвольной природы, позволяет единообразным образом изучать конкретные процедуры прикладной статистики. |
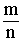 (3)
(3) . (4)
. (4)