Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Прикладная статистика: Методы оценивания параметровЧасть 2. Основные проблемы прикладной статистики 2.2. Оценивание 2.2.1. Методы оценивания параметров В прикладной статистике используются разнообразные параметрические модели. Термин «параметрический» означает, то вероятностно-статистическая модель полностью описывается конечномерным вектором фиксированной размерности. Причем эта размерность не зависит от объема выборки. Рассмотрим выборку x1, x2,…, xn из распределения с плотностью f(x;θ0), где f(x;θ0)- элемент параметрического семейства плотностей распределения вероятностей {f(x;θ), θєΘ}. Здесь Θ – заранее известное k-мерное пространство параметров, являющееся подмножеством евклидова пространства Rk, а конкретное значение параметра θ0 статистику неизвестно. Обычно в прикладной статистике применяются параметрические семейства с k = 1,2,3 (см. главу 1.2). В статистике нечисловых данных вместо плотности часто рассматриваются вероятности попадания в точки. Напомним, что в параметрических задачах оценивания принимают вероятностную модель, согласно которой результаты наблюдений x1, x2,…, xn рассматривают как реализации n независимых случайных величин. Задача оценивания состоит в том, чтобы оценить неизвестное статистику значение параметра θ0 наилучшим (в каком-либо смысле) образом. Пример 1. В статистических задачах стандартизации и управления качеством используют семейство гамма-распределений. Плотность гамма-распределения имеет вид
Плотность вероятности в формуле (1) определяется тремя параметрами a, b, c, где a>2, b>0. При этом a является параметром формы, b - параметром масштаба и с - параметром сдвига. Множитель 1/Γ(а) является нормировочным, он введен, чтобы
Здесь Γ(а) - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (1),
Подробные решения задач оценивания параметров для гамма-распределения содержатся в разработанном нами государственном стандарте ГОСТ 11,011-83 «Прикладная статистика. Правила определения оценок и доверительных границ для параметров гамма-распределения» [1]. В настоящее время эта публикация используется в качестве методического материала для инженерно-технических работников промышленных предприятий и прикладных научно-исследовательских институтов. Поскольку гамма-распределение зависит от трех параметров, то имеется 23 – 1 = 7 вариантов постановок задач оценивания. Они описаны в табл.1. Таблица 1. Постановки задач оценивания для параметров гамма-распределения
В табл.2 приведены реальные данные о наработке резцов до предельного состояния, в часах. Упорядоченная выборка (вариационный ряд) объема n = 50 взята из государственного стандарта [1]. Проверка согласия данных о наработке резцов с семейством гамма-распределений проведена в главе 2.3. Именно эти данные будут служить исходным материалом для демонстрации тех или иных методов оценивания параметров. Таблица 2. Наработка резцов до предельного состояния, ч
Выбор «наилучших» оценок в определенной параметрической модели прикладной статистики – научно-исследовательская работа, растянутая во времени. Выделим два этапа. Этап асимптотики: оценки строятся и сравниваются по их свойствам при безграничном росте объема выборки. На этом этапе рассматривают такие характеристики оценок, как состоятельность, асимптотическая эффективность и др. Этап конечных объемов выборки: оценки сравниваются, скажем, при n = 10. Ясно, что исследование начинается с этапа асимптотики: чтобы сравнивать оценки, надо сначала их построить и быть уверенными, что они не являются абсурдными (такую уверенность дает доказательство состоятельности). С какой оценки начинать? Одним из наиболее известных и простых в употреблении методов является метод моментов. Название связано с тем, что этот метод опирается на использование выборочных моментов
где x1, x2,…, xn – выборка, т.е. набор независимых одинаково распределенных случайных величин с числовыми значениями. В прикладной статистике метод анализа данных называется методом моментов, если он использует статистику
где g: Rq → Rk – некоторая функция (здесь k – число неизвестных числовых параметров). Чаще всего термин «метод моментов» используют, когда речь идет об оценивании параметров. В этом случае обычно предполагают, что плотность вероятности распределения элементов выборки f(x) входит в заранее известное статистику параметрическое семейство {f(x;θ), θєΘ}, т.е. f(x) = f(x;θ0) при некотором θ0. Здесь Θ – заранее заданное k-мерное пространство параметров, являющееся подмножеством евклидова пространства Rk, а конкретное значение параметра θ0 статистику неизвестно, его и следует оценить. Известно также, что неизвестный параметр определяется с помощью известной статистику функции через начальные моменты элементов выборки:
В методе моментов в качестве оценки θ0 используют статистику Yn вида (2), которая отличается от формулы (2) тем, что теоретические моменты заменены выборочными. Статистики Yn вида (2) применяются не только для оценивания параметров, но и для непараметрического оценивания характеристик случайной величины, таких, как коэффициент вариации, и для проверки гипотез. Во всех случаях применения статистики Yn вида (2) говорят о методе моментов. Распределение вектора Yn во всех практически важных случаях является асимптотически нормальным. Это утверждение опирается на следующий общий факт. Пусть случайный вектор Zn є Rq асимптотически нормален с математическим ожиданием z∞ и ковариационной матрицей cij/n, а функция h: Rq → R1 достаточно гладкая. Тогда случайная величина h(Zn) асимптотически нормальна с математическим ожиданием h(z∞) и дисперсией
Этот способ нахождения предельного распределения известен как δ-метод Рао [2], метод линеаризации [3]. Последний термин и будем использовать. Условия регулярности, накладываемые на распределение случайной величины Zn и функцию h, при которых метод линеаризации обоснован, хорошо известны (см. [4], [2, с.337-339], а также главу 1.4 настоящего учебника). Для получения асимптотического распределения статистики Yn вида (2) можно применить метод линеаризации к асимптотически нормальному вектору выборочных моментов (Mn1, Mn2, …, Mnq) и функции g из формулы (2). В силу многомерной центральной предельной теоремы (см. главу 1.4) указанная асимптотическая нормальность имеет место, если, например,
Это условие выполнено, в частности, для результатов измерений, распределения которых сосредоточены на ограниченных сверху и снизу интервалах. При реализации намеченного плана для применения формулы (4) необходимо использовать асимптотические дисперсии и ковариации выборочных моментов, т.е. величины, обозначенные в формуле (4) как crs . Эти величины имеют вид [2, с.388]:
Здесь μr – теоретический центральный момент порядка r, т.е.
Таким образом, для получения асимптотического распределения случайной величины Yn вида (2) достаточно знать теоретические центральные моменты результатов наблюдений и вид функции g. Отметим, что асимптотическим смещением оценок в рассматриваемом случае можно пренебречь, поскольку его вклад в средний квадрат ошибки статистической оценки – бесконечно малая величина более высокого порядка по сравнению с асимптотической дисперсией. Однако моменты неизвестны. Их приходится оценивать. В соответствии с теоремами о наследовании сходимости для нахождения асимптотического распределения функции от выборочных моментов можно воспользоваться не теоретическими моментами, а их состоятельными оценками. Эти оценки можно получить разными способами. Можно непосредственно применить формулы (5), заменив теоретические моменты выборочными. Можно выразить моменты через параметры рассматриваемого распределения. Можно применять более сложные процедуры, например, на основе непараметрических устойчивых (робастных) оценок моментов типа урезанных средних Пуанкаре и др. (в первой в России книге по общей теории устойчивости [5] проблематика робастных оценок рассмотрена в главе 2). Для оценивания параметров гамма-распределения воспользуемся известной формулой [6, с.184-185], согласно которой для случайной величины Х, имеющей гамма-распределение с параметрами формы а, масштаба b =1 и сдвига c=0,
Следовательно, M(X) = a, M(X2) = a(a+1), D(X) = M(X2) – (M(X))2 = a(a+1) – a2 = a. Найдем третий центральный момент M(X – M(X))3. Справедливо равенство M(X – M(X))3 = M(X3) – 3 M(X2) M(X) + 3 M(X) (M(X))2 - (M(X))3. Из равенства (6) вытекает, что M(X – M(X))3 = a(a+1)(a+2) – 3 a (a+1) a + 3 a a2 – a3 = 2a. Если Y – случайная величина, имеющая гамма-распределение с произвольными параметрами формы a, масштаба b и сдвига c, то Y = bX + c. Следовательно, M(Y) = ab+c, D(Y) = ab2, M(Y – M(Y))3 = 2 a b3. Пример 2. Оценивание методом моментов параметров гамма-распределения в случае трех неизвестных параметров (строка 7 таблицы 1). В соответствии с проведенными выше рассуждениями для оценивания трех параметров достаточно использовать три выборочных момента – выборочное среднее арифметическое
выборочную дисперсию
и выборочный третий центральный момент
Приравнивая теоретические моменты, выраженные через параметры распределения, и выборочные моменты, получаем систему уравнений метода моментов:
Решая эту систему, находим оценки метода моментов. Подставляя второе уравнение в третье, получаем оценку метода моментов для параметра сдвига:
Подставляя эту оценку во второе уравнение, находим оценку метода моментов для параметра формы:
Наконец, из первого уравнения находим оценку для параметра сдвига:
Для реальных данных [1], приведенных выше в табл.2, выборочное среднее арифметическое Оценки параметров гамма-распределения, полученные методом моментов, являются функциями от выборочных моментов. В соответствии со сказанным выше они являются асимптотически нормальными случайными величинами. Их распределения аппроксимируются нормальными распределениями, математические ожидания которых равны соответствующим параметрам, а дисперсии находятся с помощью формулы (4) с учетом формул (5) и (6). В табл.3 приведены оценки метода моментов и их асимптотические дисперсии при различных вариантах сочетания известных и неизвестных параметров гамма-распределения. Таблица 3. Оценки метода моментов и их асимптотические дисперсии
Примечание. При описании вероятностной модели известные статистику параметры отмечены плюсами, оцениваемые – минусами. Все оценки метода моментов, приведенные в табл.3, включены в государственный стандарт [1]. Они охватывают все постановки задач оценивания параметров гамма-распределения (см. табл.1) , кроме тех, когда неизвестен только один параметр – a или b. Для этих исключительных случаев в [1] разработаны специальные методы оценивания. Поскольку асимптотическое распределение оценок метода моментов известно, то не представляет труда формулировка правил проверки статистических гипотез относительно значений параметров распределений, а также построение доверительных границ для параметров. Например, в вероятностной модели, когда все три параметра неизвестны, в соответствии с третьей строкой таблицы 3 нижняя доверительная граница для параметра а, соответствующая доверительной вероятности γ = 0,95, в асимптотике имеет вид
а верхняя доверительная граница для той же доверительной вероятности такова
где а* - оценка метода моментов параметра формы (табл.3). Метод моментов является универсальным. Однако получаемые с его помощью оценки лишь в редких случаях обладают оптимальными свойствами. Поэтому в прикладной статистике применяют и другие виды оценок. В работах, предназначенных для первоначального знакомства с математической статистикой, обычно рассматривают оценки максимального правдоподобия (сокращенно ОМП):
Таким образом, сначала строится плотность распределения вероятностей, соответствующая выборке. Поскольку элементы выборки независимы, то эта плотность представляется в виде произведения плотностей для отдельных элементов выборки. Совместная плотность рассматривается в точке, соответствующей наблюденным значениям. Это выражение как функция от параметра (при заданных элементах выборки) называется функцией правдоподобия. Затем тем или иным способом ищется значение параметра, при котором значение совместной плотности максимально. Это и есть оценка максимального правдоподобия. Хорошо известно, что оценки максимального правдоподобия входят в класс наилучших асимптотически нормальных оценок (определение дано ниже). Однако при конечных объемах выборки в ряде задач ОМП недопустимы, т.к. они хуже ( дисперсия и средний квадрат ошибки больше), чем другие оценки, в частности, несмещенные [6]. Именно поэтому в ГОСТ 11.010-81 для оценивания параметров отрицательного биномиального распределения используются несмещенные оценки, а не ОМП [7]. Из сказанного следует априорно предпочитать ОМП другим видам оценок можно – если можно – лишь на этапе изучения асимптотического поведения оценок. В отдельных случаях ОМП находятся явно, в виде конкретных формул, пригодных для вычисления. Пример 3. Найдем ОМП для выборки из нормального распределения, каждый элемент которой имеет плотность
Таким образом, надо оценить двумерный параметр (m, σ2). Произведение плотностей вероятностей для элементов выборки, т.е. функция правдоподобия, имеет вид
Требуется решить задачу оптимизации
Как и во многих иных случаях, задача оптимизации проще решается, если прологарифмировать функцию правдоподобия, т.е. перейти к функции
называемой логарифмической функцией правдоподобия. Для выборки из нормального распределения
Необходимым условием максимума является равенство 0 частных производных от логарифмической функции правдоподобия по параметрам, т.е.
Система (10) называется системой уравнений максимального правдоподобия. В общем случае число уравнений равно числу неизвестных параметров, а каждое из уравнений выписывается путем приравнивания 0 частной производной логарифмической функции правдоподобия по тому или иному параметру. При дифференцировании по m первые два слагаемых в правой части формулы (9) обращаются в 0, а последнее слагаемое дает уравнение
Следовательно, оценкой m* максимального правдоподобия параметра m является выборочное среднее арифметическое,
Для нахождения оценки дисперсии необходимо решить уравнение
Легко видеть, что
Следовательно, оценкой (σ2)* максимального правдоподобия для дисперсии σ2 с учетом найденной ранее оценки для параметра m является выборочная дисперсия,
Итак, система уравнений максимального правдоподобия решена аналитически, ОМП для математического ожидания и дисперсии нормального распределения – это выборочное среднее арифметическое и выборочная дисперсия. Отметим, что последняя оценка является смещенной. Отметим, что в условиях примера 3 оценки метода максимального правдоподобия совпадают с оценками метода моментов. Причем вид оценок метода моментов очевиден и не требует проведения каких-либо рассуждений. В большинстве случаев аналитических решений не существует, для нахождения ОМП необходимо применять численные методы. Так обстоит дело, например, с выборками из гамма-распределения или распределения Вейбулла-Гнеденко. Во многих работах каким-либо итерационным методом решают систему уравнений максимального правдоподобия ([8] и др.) или впрямую максимизируют функцию правдоподобия типа (8) (см. [9] и др.). Однако применение численных методов порождает многочисленные проблемы. Сходимость итерационных методов требует обоснования. В ряде примеров функция правдоподобия имеет много локальных максимумов, а потому естественные итерационные процедуры не сходятся [10]. Для данных ВНИИ железнодорожного транспорта по усталостным испытаниям стали уравнение максимального правдоподобия имеет 11 корней [11]. Какой из одиннадцати использовать в качестве оценки параметра? Как следствие осознания указанных трудностей, стали появляться работы по доказательству сходимости алгоритмов нахождения оценок максимального правдоподобия для конкретных вероятностных моделей и конкретных алгоритмов. Примером является статья [12]. Однако теоретическое доказательство сходимости итерационного алгоритма – это еще не всё. Возникает вопрос об обоснованном выборе момента прекращения вычислений в связи с достижением требуемой точности. В большинстве случаев он не решен. Но и это не все. Точность вычислений необходимо увязывать с объемом выборки – чем он больше, тем точнее надо находить оценки параметров, в противном случае нельзя говорить о состоятельности метода оценивания. Более того, при увеличении объема выборки необходимо увеличивать и количество используемых в компьютере разрядов, переходить от одинарной точности расчетов к двойной и далее – опять-таки ради достижения состоятельности оценок. Таким образом, при отсутствии явных формул для оценок максимального правдоподобия нахождение ОМП натыкается на ряд проблем вычислительного характера. Специалисты по математической статистике позволяют себе игнорировать все эти проблемы, рассуждая об ОМП в теоретическом плане. Однако прикладная статистика не может их игнорировать. Отмеченные проблемы ставят под вопрос целесообразность практического использования ОМП. Нет необходимости абсолютизировать ОМП. Кроме них, существуют другие виды оценок, обладающих хорошими статистическими свойствами. Примером являются одношаговые оценки (ОШ-оценки). В прикладной статистике разработано много видов оценок. Упомянем квантильные оценки. Они основаны на идее, аналогичной методу моментов, но только вместо выборочных и теоретических моментов приравниваются выборочные и теоретические квантили. Другая группа оценок базируется на идее минимизации расстояния (показателя различия) между эмпирическими данными и элементом параметрического семейства. В простейшем случае минимизируется евклидово расстояние между эмпирическими и теоретическими гистограммами, а точнее, векторами, составленными из высот столбиков гистограмм. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
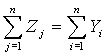 (1)
(1)