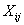Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Орлов А.И. Эконометрика: Основы статистического контроля качества продукцииГлава 13. Эконометрические методы управления качеством и сертификации продукции 13.1. Основы статистического контроля качества продукции Сначала дадим общие сведения о месте статистических методов в управлении качеством и сертификации продукции. Затем рассмотрим центральную тему эконометрики качества - статистический контроль качества продукции. Продемонстрируем его высокую экономическую эффективность. Качество продукции и рыночная экономика. Руководители и специалисты промышленных предприятий хотят не только выжить, но и выиграть в борьбе с конкурентами. Более частными задачами, которые они хотят решить, обычно являются: - выйти на международный рынок; - поднять качество продукции до японского уровня; - полностью ликвидировать рекламации, и т.д. Для решения этих задач им надо повышать качество продукции. Все руководители и специалисты промышленных предприятий это хорошо знают, слова "сертификация", "международные стандарты ИСО серии 9000 по системам качества" уже навязли в зубах. Менее осознано, что управление качеством - это прежде всего применение современных статистических методов. На Западе (США) и на Востоке (Япония) это - аксиома. Вот типичное высказывание японского менеджера и инженера: "Методы статистики - именно то средство, которое необходимо изучить, чтобы внедрить управление качеством. Они - наиболее важная составная часть комплексной системы всеобщего управления качеством на фирме. В японских корпорациях все, начиная от председателя Совета Директоров и до рядового рабочего в цехе, обязаны знать хотя бы основы статистических методов." Так считает Каору Исикава, президент промышленного института Мусаси, заслуженный профессор Токийского университета (цитируется по японскому пособию по статистическим методам обеспечения качества [1, с.15]). Раз все японские работники знают про статистические методы - значит, их научили в школе. Во всем мире - в США, Японии и Ботсване - школьники учат статистические методы как один из обязательных школьных предметов, вместе с физикой, химией, математикой и историей. ЮНЕСКО регулярно проводит конференции по преподаванию статистики в средней школе. И вот всем виден результат - качество компьютеров IBM и японских телевизоров. А отечественные бюрократы десятилетиями "боролись за качество" (вспомните, была "пятилетка эффективности и качества"!), "внедряли" кипы бумаг - КС УКП ... (популярное сочетание в 1970-е и 1980-е годы: КС УКП - это Комплексная Система Управления Качеством Продукции; имелись областные варианты - горьковская, львовская, днепропетровская и т.д.). Справедливости ради надо отметить, что популярные ныне международные стандарты ИСО серии 9000 ничем принципиально не отличаются от давних документов КС УКП, а в некоторых отношениях КС УКП были более прогрессивными, чем нынешние стандарты ИСО 9000. В очередной раз придуманное в нашей стране попало на Запад, было там оформлено по-другому, а потом стало внедряться у нас как последнее достижение западной цивилизации… ИТОГ НА СЕГОДНЯ: весь мир, кроме нас, знает статистические методы и повсеместно применяет их для повышения качества. Мы вынуждены догонять. Очевидно, овладение основами статистического контроля качества продукции - неотъемлемая часть экономического и тем более эконометрического образования. О сертификации. Вслед за т. н. развитыми странами в России намечается всё расширяющаяся тенденция к сертификации продукции, т.е. к официальной гарантии поставки производителем продукции, удовлетворяющей установленным требованиям. Средства массовой информации отмечают, что в условиях рыночной экономики поставщики и продавцы должны иметь сертификаты качества на предлагаемые ими товары и услуги. Маркетинг, т.е. "производственная и коммерческая политика, нацеленная на получение максимальной прибыли на основе изучения рынка, создания конкурентоспособной продукции и её полной реализации" (определение взято из выпущенной нашим Центром брошюры [2, с.64-65]), включает в себя работы по сертификации. За новыми терминами зачастую скрываются хорошо известные понятия, несколько модернизированные в соответствии с современной обстановкой. Так, целесообразно связать комплексную систему управления качеством продукции с маркетингом: "маркетинг в широком смысле - это усовершенствованная, ориентированная на рыночную экономику КС УКП" [2,с.61]. Есть несколько уровней сертификации. Говоря о сертификации продукции, могут иметь в виду качество конкретной её партии. В ряде случаев это оправдано - рядового потребителя интересует качество лишь той единицы продукции, которую он сам приобрёл. Однако установление долговременных хозяйственных связей целесообразно лишь в случае, когда поставщик гарантирует высокое качество не одной, а всех партий своей продукции. Очевидно, для этого должны быть проведены оценка и сертификация технологических процессов и производств, обеспечивающих выпуск этой продукции. Ещё больше повышается доверие к поставщику, если не только отдельные технологические процессы, но и всё предприятие в целом гарантированно выпускает продукцию высокого качества. Это обеспечивается действующей на предприятии системой качества, удовлетворяющей требованиям Международной организации по стандартизации (International Standartization Organization, сокращенно ISO, по-русски - ИСО), выраженным в системе стандартов ИСО 9000, о которых уже шла речь. В условиях рыночной экономики основная характеристика товара - его конкурентоспособность. Очевидно, производителю необходимо уметь оценивать конкурентоспособность перед запуском продукции в производство или началом работы по продвижению на зарубежный рынок. Одним из основных компонентов конкурентоспособности является технический уровень продукции. Фирма, обладающая патентом или новой научно-технической разработкой, имеет более высокий излишек производителя по сравнению с другими фирмами. При выборе направления инвестиционных вложений одна из основных учитываемых характеристик - технический уровень продукции. Из сказанного вытекает, что сертификация продукции - это современная форма управления качеством продукции. На Западе общепринято, что основная составляющая в управлении качеством продукции - это статистические методы (см., например, отчет Комитета ИСО по изучению принципов стандартизации [3]). В нашей стране внедрение комплексных систем управления качеством (КС УКП), как уже отмечалось, сводилось во многом к подготовке документации организационного характера. Статистические методы использовались в промышленности недостаточно, а государственные стандарты по этой тематике зачастую содержали грубейшие ошибки (см. ниже). Подготовка предприятий к сертификации продукции, технологических процессов и производств, систем качества требует приложения труда квалифицированных специалистов, причем в достаточно большом объеме. Подобную работу обычно проводят специализированные организации. О развитии статистических методов сертификации в России. Около 150 лет статистические методы применяются в России для проверки соответствия продукции установленным требованиям, т.е. для сертификации. Так, еще в 1846 г. действительный член Петербургской академии наук М.В. Остроградский рассматривал задачу статистического контроля партий мешков муки или штук сукна армейскими поставщиками. С тех пор в России в статистическом контроле качества было сделано многое, особенно в области теории: Так, солидные монографии проф. Ю.К. Беляева и проф. Я.П. Лумельского можно смело назвать классическими. Был выпущен и длинный ряд практических руководств, в основном переводных. С начала 1970-х годов стали разрабатываться государственные стандарты по статистическим методам. В связи с обнаружением в них грубых ошибок 24 из 31 государственного стандарта по статистическим методам были отменены в 1986-87 гг. (перечень стандартов и описание ошибок приведены в работе [4]). К сожалению, потеряв правовую силу как нормативные документы, ошибочные стандарты продолжают использоваться как научно-технические издания. В 1989 г. был организован Центр статистических методов и информатики (ЦСМИ) для работ по развитию и внедрению современных статистических методов. Уже к середине 1990 г. ЦСМИ были разработаны 7 диалоговых систем по современным статистическим методам управления качеством, а именно, СПК, АТСТАТ-ПРП, СТАТКОН, АВРОРА-РС, ЭКСПЛАН, ПАСЭК, НАДИС (описания этих систем даны в работе [5]). Параллельно ЦСМИ вел работу по объединению статистиков. В апреле 1990 г. в Большом Актовом Зале Московского Энергетического института прошла Учредительная конференция Всесоюзной организации по статистическим методам и их применениям. На Учредительном съезде Всесоюзной статистической ассоциации (ВСА) в октябре 1990 г. в Московском экономико-статистическом институте эта организация вошла в состав ВСА в качестве секции статистических методов. В 1992г. после развала СССР и фактического прекращения работы ВСА на основе секции статистических методов ВСА организована Российская ассоциация по статистическим методам (РАСМ), а затем и Российская академия статистических методов, существующие и в настоящее время. В мероприятиях секции статистических методов ВСА и РАСМ активно участвовали несколько сот человек. Основной тематикой работ многих из этих специалистов являются статистические методы в сертификации (управлении качеством). В ЦСМИ и РАСМ, объединивших большинство ведущих российских специалистов, коллективными усилиями разработан единый подход к проблемам применения статистических методов в сертификации и управлении качеством. Статистический контроль - это выборочный контроль на научной основе. Контроль качества продукции всем знаком хотя бы по названию - им обычно занимается отдел технического контроля (ОТК) предприятия. Есть различные виды контроля - входной контроль, приемочный контроль (готовой продукции), и контроль при передаче полуфабрикатов и комплектующих из цеха в цех. Кроме сплошного контроля всех изделий подряд применяют выборочный, когда о качестве партии продукции судят по результатам контроля некоторой части - выборки. Зачем нужен выборочный контроль? Чтобы проверить качество спички - надо чиркнуть ею. Загорится - должное качество, не загорится - брак. Но повторно однажды зажженную спичку использовать уже нельзя. Поэтому партию спичек можно контролировать только выборочно. Партии консервов, лампочек, патронов - тоже. Т.е. при разрушающем контроле необходимо пользоваться выборочными методами и судить о качестве партии продукции по результатам контроля её части - выборки. Выборочные методы контроля могут применяться и из экономических соображений, когда стоимость контроля высока по сравнению со стоимостью изделия. Например, вряд ли целесообразно визуально проверять качество каждой скрепки в каждой коробке. Для проведения выборочного контроля необходимо сформировать выборку, выбрать план контроля. А если план имеется - полезно знать его свойства. Анализ и синтез планов проводят с помощью математического моделирования на основе теории вероятностей и математической статистики, применяя компьютерные диалоговые системы (пакеты программ). Зачем нужны диалоговые системы по статистическому контролю? Раньше, действительно, ОТК формально применяли планы контроля из ГОСТов на конкретную продукцию, а реальное качество выпускаемых изделий никого не интересовало. Сейчас - ситуация начинает меняться. С декабря 1990 г. обязательность большинства ГОСТов отменена (в части основных показателей качества, кроме показателей безопасности). У промышленности сняты кандалы. Но - со становлением рыночной экономики появляются конкуренты. В том числе зарубежные. Руководителям производства приходится отлаживать систему контроля качества не для галочки, не по приказу обкома, а для повышения доходов предприятий. А потому - и собственных тоже. Компьютерные диалоговые системы позволяют прежде всего проводить анализ и синтез планов контроля. Пусть перед Вами - прежний ГОСТ на продукцию, в нем есть раздел "Правила приемки" с планами контроля. Хороша эта система планов или плоха? С помощью диалоговых систем Вы найдете характеристики конкретного плана, приемочный и браковочный уровни дефектности (см. ниже) и т.д. Можно провести и синтез планов, т.е. компьютер подберет план, удовлетворяющий Вашим условиям. Российской ассоциацией статистических методов были проанализированы сотни стандартов на конкретную продукцию (разделы "Правила приемки") и ГОСТы по статистическим методам. Обнаружено, что более половины и тех и других стандартов содержат грубые ошибки, пользоваться ими нельзя. Причины этого печального положения проанализированы в статье [4]. В отличие от ГОСТов, диалоговым системам ЦСМИ по статистическому контролю верить можно и нужно. И экономически выгодно. По оценкам, полученным в работе [6], применение современных статистических методов позволяет в среднем вдвое сократить трудозатраты на контрольные операции (как известно, на них расходуют примерно 10% от стоимости машиностроительной продукции). Следовательно, от внедрения современных эконометрических методов обеспечения качества продукции Россия может получить более 5 миллиардов долларов США дополнительного дохода в год. Приведем ещё два сообщения о высокой экономической эффективности статистического контроля. "Мы документально зафиксировали экономию от применения методов статистического контроля и методов разрешения проблем, которым обучили наших сотрудников. Мы приближаемся к степени окупаемости около 30 долларов на 1 вложенный доллар. Вот почему мы получили такую серьезную поддержку от высшего руководства", - сообщает Билл Виггенхорн, ответственный за подготовку специалистов фирмы "Моторола" (цитируем по статье [7]). По подсчетам профессора Массачусетского технологического института Фримена (см. монографию [8]), только статистический приемочный контроль давал промышленности США 4 миллиарда долларов в 1958 г. (это более 20 миллиарда долларов в ценах 2001 г.), т.е. 0,8% ВВП - Валового Внутреннего Продукта. На наш взгляд, российским предпринимателям и менеджерам промышленных предприятий целесообразно равняться на японских коллег - знать хотя бы основы статистических методов, т.е. эконометрики, и активно их применять, постоянно консультируясь со специалистами-эконометриками. Основы статистического контроля. Выборочный контроль, построенный на научной основе, т.е. исходящий из теории вероятностей и математической статистики, называют статистическим контролем. Предпринимателя и менеджера выборочный контроль может интересовать не только в связи с качеством продукции, но и в связи, например, с контролем экологической обстановки, поскольку зафиксированные государственными органами экологические нарушения влекут штрафы и иные "неприятные" последствия. Обсудим основные подходы статистического контроля. При статистическом контроле решение о генеральной совокупности – об экологической обстановке в данном регионе или о партии продукции - принимается по выборке, состоящей из некоторого количества единиц (единиц экологического контроля или единиц продукции). Следовательно, выборка должна представлять партию, т.е. быть репрезентативной (представительной). Как эти слова понимать, как проверить репрезентативность? Ответ может быть дан лишь в терминах вероятностных моделей выборки. Наиболее распространенными являются две вероятностные модели—биномиальная и гипергеометрическая. В биномиальной модели предполагается, что результаты контроля n единиц можно рассматривать как совокупность n независимых одинаково распределенных случайных величин Х1, Х2,....,Хn , где Хi = 1, если i‑ое измерение показывает, что есть нарушение, т.е. превышено ПДК (предельная норма концентрации) или i‑ое изделие дефектно, и Хi= 0, если это не так. Тогда число Х превышений ПДК или дефектных единиц продукции в партии равно Х= Х1+ Х2+...+ Хn .(1) Из формулы (1) и Центральной Предельной Теоремы теории вероятностей вытекает, что при увеличении объема выборки n распределение Х сближается с нормальным распределением. Известно, что распределение Х имеет вид Р( Х= k) = Cnk pk (1—p)n-k , (2) где Cnk - число сочетаний из n элементов по k, а p —уровень дефектности (в другой предметной области - доля превышений ПДК в генеральной совокупности), т.е. p = Р( Хi= 1). Формула (2) задает так называемое биномиальное распределение. Гипергеометрическое распределение соответствует случайному отбору единиц в выборку. Пусть среди N единиц, составляющих генеральную совокупность, имеется D дефектных. Случайность отбора означает, что каждая единица имеет одинаковые шансы попасть в выборку. Мало того, ни одна пара единиц не должна иметь при отборе в выборку преимущества перед любой другой парой. То же самое —для троек, четверок и т.д. Это условие выполнено тогда и только тогда, когда каждое из Отбор случайной выборки согласно описанным правилам организуют при проведении различных лотерей. Пусть Y —число дефектных единиц в случайной выборке, организованной таким образом. Известно, что тогда P (Y = k) – гипергеометрическое распределение, т.е.
Замечательный математический результат состоит в том, что биномиальная и гипергеометрическая модели весьма близки, когда объем генеральной совокупности (партии) по крайней мере в 10 раз превышает объем выборки. Другими словами, можно принять, что Р( Х = k) = P ( Y = k ), (4) если объем выборки мал по сравнению с объемом партии. При этом в качестве p в формуле (4) берут D/N. Близость результатов, получаемых с помощью биномиальной и гипергеометрической моделей, весьма важна с философской точки зрения. Дело в том, что эти модели исходят из принципиально различных философских предпосылок. В биномиальной модели случайность присуща каждой единице - она с какой-то вероятностью дефектна, а с какой-то - годна. В то же время в гипергеометрической модели качество определенной единицы детерминировано, задано, а случайность проявляется лишь в отборе, вносится экологом или экономистом при составлении выборки. В науках о человеке противоречие между аналогичными моделями выборки еще более выражено. Биномиальная модель предполагает, что поведение человека, в частности, выбор им определенного варианта при ответе на вопрос, определяется с участием случайных причин. Например, человек может случайно сказать «да», случайно—«нет». Некоторые философы отрицают присущую человеку случайность. Они верят в причинность и считают поведение конкретного человека практически полностью детерминированным. Поэтому они принимают гипергеометрическую модель и считают, что случайность отличия ответов в выборке от ответов во всей генеральной совокупности определяется всецело случайностью, вносимой при отборе единиц наблюдения в выборку. Соотношение (4) показывают, что во многих случаях нет необходимости принимать чью-либо сторону в этом споре, поскольку обе модели дают близкие численные результаты. Отличия проявляются при обсуждении вопроса о том, какую выборку считать представительной. Является ли таковой выборка, составленная из 20 изделий, лежащих сверху в первом вскрытом ящике? В биномиальной модели - да, в гипергеометрической - нет. Биномиальная модель легче для теоретического изучения, поэтому будем её рассматривать в дальнейшем. Однако при реальном контроле лучше формировать выборку, исходя из гипергеометрической модели. Это делают, выбирая номера изделий (для включения в выборку) с помощью датчиков псевдослучайных чисел на ЭВМ (см. главу 11) или с помощью таблиц псевдослучайных чисел. Алгоритмы формирования выборки встраивают в современные программные продукты по статистическому контролю. Планы статистического контроля и правила принятия решений. Под планом статистического контроля понимают алгоритм, т.е. правила действий, на входе при этом—генеральная совокупность (партия продукции), а на выходе—одно из двух решений: «принять партию» либо «забраковать партию». Рассмотрим несколько примеров. Одноступенчатые планы контроля (n,c): отобрать выборку объема n; если число дефектных единиц в выборке X не превосходит c, то партию принять, в противном случае забраковать. Число с называется приемочным. Частные случаи: план (n,0) —партию принять тогда и только тогда, когда все единицы в выборке являются годными; план (n,1) - партия принимается, если в выборке все единицы являются годными или ровно одно - дефектное, во всех остальных случаях партия бракуется. Двухступенчатый план контроля (n,a,b) + (m,c): отобрать первую выборку объема n; если число дефектных единиц в первой выборке X не превосходит a , то партию принять; если число дефектных единиц в первой выборке X больше или равно b, то партию забраковать; во всех остальных случаях, т.е. когда Х больше a, но меньше b, следует взять вторую выборку объема m; если число дефектных единиц во второй выборке Y не превосходит c, то партию принять, в противном случае забраковать. Рассмотрим в качестве примера план (20, 0, 2) + (40, 0). Сначала берется первая выборка объема 20. Если все единицы в ней - годные, то партия принимается. Если две или больше - дефектные, партия бракуется. А если только одно - дефектное? В реальной ситуации в таких случаях начинаются споры между представителями предприятия и экологического контроля, или поставщика и потребителя. Говорят, например, что дефектная единица случайно попала в партию, что ее подсунули конкуренты или что при контроле случайно сделан неправильный вывод. Поэтому, чтобы споры пресечь, берут вторую выборку объема 40 (вдвое большего, чем в первый раз). Если все единицы во второй выборке - годные, то партию принимают, в противном случае - бракуют. В реальной нормативно-технической документации - договорах на поставку, стандартах, технических условиях, инструкциях по экологическому контролю и т.д. - не всегда четко сформулированы планы статистического контроля и правила принятия решений. Например, при описании двухступенчатого плана контроля вместо задания приемочного числа с может стоять загадочная фраза "результат контроля второй выборки считается окончательным". Остается гадать, как принимать решение по второй выборке. Менеджер, администратор (государственный служащий), эколог или экономист, занимающийся вопросами экологического контроля или контроля качества, должен первым делам добиваться кристальной ясности в формулировках правил принятия решений, иначе ошибочные и необоснованные решения, а потому и убытки неизбежны. Оперативная характеристика плана статистического контроля. Каковы свойства плана статистического контроля? Они, как правило, определяются с помощью функции f(p), связывающей вероятность p дефектности единицы контроля с вероятностью f(p) положительной оценки экологической обстановки (приемки партии) по результатам контроля. При этом вероятность p того, что конкретная единица дефектна, называется входным уровнем дефектности, а указанная функция называется оперативной характеристикой плана контроля. Если дефектные единицы отсутствуют, р = 0, то партия всегда принимается, т.е. f(0) = 1. Если все единицы дефектные, р = 1, то партия наверняка бракуется, f(1) = 0. Между этими крайними значениями р функция f(p) монотонно убывает. Вычислим оперативную характеристику плана (n,0). Поскольку партия принимается тогда и только тогда, когда все единицы являются годными, а вероятность того, что конкретная единица—годная, равна (1‑р), то оперативная характеристика имеет вид f(p) = Р(Х=0) = (1—р)n. (5) Для плана (n,1) оперативная характеристика, как легко видеть, такова: f(p) = Р(Х=0)+Р(Х=1) = (1—р)n + n (1—р)n-1 (6) Оперативные характеристики для конкретных планов статистического контроля не всегда имеют такой простой вид, как в случае формул (5) и (6). Рассмотрим в качестве примера план (20, 0, 2) + (40, 0). Сначала найдем вероятность того, что партия будет принята по результатам контроля первой партии. Согласно формуле (5) имеем: f1(p) = Р(Х=0) = (1—р)20. Вероятность того, что понадобится контроль второй выборки, равна Р(Х=1) = 20(1—р)19. При этом вероятность того, что по результатам её контроля партия будет принята, равна f2(p) = Р(Х=0) = (1—р)40. Следовательно, вероятность того, что партия будет принята со второй попытки, т.е. что при контроле первой выборки обнаружится ровно одна дефектная единица, а затем при контроле второй—ни одной, равна f3(p) = Р(Х=1) f2(p) = 20(1—р)19(1—р)40= 20(1—р)59. Следовательно, вероятность принятия партии с первой или со второй попытки равна f(p) = f1(p) + f3(p) = (1—р)20+ 20(1—р)59. При практическом применении методов статистического приемочного контроля для нахождения оперативных характеристик планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы. Риск поставщика и риск потребителя, приемочный и браковочный уровни дефектности. С оперативной характеристикой связаны важные понятия приемочного и браковочного уровней дефектности, а также понятия "риск поставщика" и "риск потребителя". Чтобы ввести эти понятия, на оперативной характеристике выделяют две характерные точки, делящие входные уровни дефектности на три зоны—А, Б и В. В зоне А все почти всегда хорошо, а именно - почти всегда экологическая обстановка признается благополучной, почти все партии принимаются. В зоне В, наоборот, почти всегда все плохо, а именно - почти всегда экологический контроль констатирует экологические нарушения, почти все партии бракуются. Зона. Б - буферная, переходная, промежуточная, в ней как вероятность приемки, так и вероятность браковки заметно отличаются от 0 и 1. Для задания границ между зонами выбирают два малых числа—риск поставщика (производителя, предприятия) f(pпp) = 1— Таким образом, если входной уровень дефектности не превосходит pпp, то вероятность забракования партии мала, т.е. не превосходит Если же входной уровень дефектности больше браковочного уровня дефектности pбр, то нарушения почти наверняка фиксируются, партия почти всегда бракуется, т.е. экологи узнают о нарушениях, потребитель оказывается защищен от попадания к нему партий со столь высоким уровнем брака. Поэтому можно сказать, что в зоне В соблюдаются интересы потребителей - брак к ним не попадает. При выборе плана контроля часто начинают с выбора приемочного и браковочного уровней дефектности. При этом выбор конкретного значения приемочного уровня дефектности отражает интересы поставщика, а выбор конкретного значения браковочного уровня дефектности - интересы потребителя. Можно доказать, что для любых положительных чисел f(pпp) > 1 - При практических расчетах обычно принимают Вычислим приемочный и браковочный уровни дефектности для плана (n,0). Из формул (5) и (7) вытекает, что (1 - pпp)n = 1 - Поскольку риск поставщика
вытекает приближенная формула pпp Для браковочного уровня дефектности имеем pбр = 1 - При практическом применении методов статистического приемочного контроля для нахождения приемочных и браковочных уровней дефектности планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы, имеющиеся в нормативно-технической документации или научно-технических публикациях. Предел среднего выходного уровня дефектности. Обсудим судьбу забракованной партии продукции. В зависимости от ситуации эта судьба может быть разной. Партия может быть утилизирована. Например, забракованная партия гвоздей может быть направлена на переплавку. У партии может быть понижена сортность, и она может быть продана по более низкой цене (при этом результаты выборочного контроля будут использованы не для проверки того, что выдержан заданный уровень качества, а для оценки реального уровня качества). Наконец, партия продукции может быть подвергнута сплошному контролю (для этого обычно привлекают инженеров из всех заводских служб). При сплошном контроле все дефектные изделия обнаруживаются и либо исправляются на месте, либо извлекаются из партии. В результате в партии остаются только годные изделия. Такая процедура называется "контроль с разбраковкой". При среднем входном уровне дефектности р и применении контроля с разбраковкой с вероятностью f(p) партия принимается (и уровень дефектности в ней по-прежнему равен р) и с вероятностью (1- f(p)) бракуется и подвергается сплошному контролю, в результате чего к потребителю поступают только годные изделия. Следовательно, по формуле полной вероятности средний выходной уровень дефектности равен f1(p)= pf(p) +0(1 - f(p)) = pf(p). Средний выходной уровень дефектности f1(p) равен 0 при р=0 и р=1, положителен на интервале (0;1), а потому достигает на нем максимума, который в теории статистического контроля называется пределом среднего выходного уровня дефектности (сокращенно ПСВУД): ПСВУД = Пример. Рассмотрим план (n,0). Для него f(p) = (1 - p)n и f1(p) = p(1-p)n. Чтобы найти ПСВУД, надо приравнять 0 производную среднего выходного уровня дефектности по среднему входному уровню дефектности:
В полученном уравнении корень р = 1 соответствует минимуму, а не максимуму. Поскольку непрерывная функция на замкнутом отрезке достигает максимума, то максимум достигается при
Следовательно, ПСВУД = По выражению (8) могут быть проведены конкретные расчеты. Однако оно довольно громоздко. Его можно упростить, используя один замечательный предел из курса математического анализа, а именно:
Сравнивая соотношения (8) и (9), видим, что ПСВУД = Первая скобка равна 1/n, а вторая согласно соотношению (9) приближается к 0,368 при росте объема выборки. Поэтому получаем простую асимптотическую формулу ПСВУД Для более сложных планов ПСВУД рассчитывают с помощью более или менее сложных компьютерных программ. При рассмотрении основ статистического контроля в настоящем пункте расчетные формулы удалось получить лишь для простейших планов, в основном для планов вида (n,0). Если ослабить требования и рассчитывать не на точные формулы, а на асимптотические, при |