 Главная страница -->
Главная страница -->  Экономические научные работы (книги)
Экономические научные работы (книги)
Зубанов Н.В. Анализ устойчивости относительно поставленной цели как один из подходов к описанию функционирования организации в условиях неопределенности: Краткая история и современное состояние проблемыГЛАВА 1. КРАТКАЯ ИСТОРИЯ И СОВРЕМЕННОЕ СОСТОЯНИЕ ПРОБЛЕМЫ В экономической теории неопределенность чаще всего считалась изначально присущей реальной среде функционирования экономической системы. Однако благодаря специфике экономической теории как научного направления этот, в общем, правильный подход не принес больших результатов в данной области. Одним из немногих случаев использования категории неопределенности для объяснения экономических явлений экономистами-теоретиками можно считать трактование феномена прибыли американским ученым Ф. Найтом как вознаграждения, получаемое предпринимателем за то, что он принимает на себя риск неудачи коммерческой операции [10, c. 195]. Й. Шумпетер, объяснявший существование прибыли как вознаграждения предпринимателя за инновационную деятельность, связывает прибыль с динамичностью реальной экономики, т.е. лишь очень косвенным образом говорит о неопределенности. Интересен подход К.К. Вальтуха к трактованию феномена стоимости товара как функции от количества информации, содержащемся в данном товаре [13]. При этом информация понимается в широком смысле, как мера распространенности однородных объектов в некотором пространстве относительно распространенности других объектов. Вальтух исходит из того, что в процессе производственной деятельности человек «систематически создает из предметов, находимых в природе, такие продукты, которые либо совсем не порождаются спонтанным природным формообразованием, либо порождаются лишь сравнительно редко»[13, c. 130]. То есть, по Вальтуху, «производство есть производство информации»[13, c. 131]. Информация, в свою очередь, определенная как мера многообразия, связана с неопределенностью динамически, через зависимость между числом возможных исходов некоторого явления или процесса и вероятностями их появления. Классическая формула информации имеет вид: I = -pi×ln(pi) (1.1) где pi – вероятности возможных исходов явления или процесса. Если в экономической теории исследование проблем, связанных с неопределенностью, не получило широкого распространения, в конкретных экономических науках, основывающихся на фундаментальных положениях экономической теории, неопределенность и риск были исследованы сквозь призму предмета и метода этих наук. В страховом деле различные виды риска составляют ядро предмета исследования этой дисциплины. Однако область исследования страхового дела смещена в сторону экономических аспектов борьбы с наступлением рисковых ситуаций и покрытия ущерба, причиненного в результате рисковых ситуаций, что не отвечает постановке задачи данного исследования. Поэтому проблемы страхования не будут затронуты. В теории общего и организационного управления, использование категорий риска и неопределенности и с ними связанных широко распространено, что, возможно, связано с необходимостью принятия научно обоснованных решений в условиях неопределенности. Это связано с бурным развитием производительных сил в XX веке, повлекшим за собой увеличение числа и ущерба от техногенных и финансовых катастроф. На этом фоне существовавшие методы организационного управления отчетливо показали свое несовершенство и нуждались в изменениях и дополнениях. В конце 40-х годов XX века в США появилась новая наука – исследование операций, возникшая на стыке математики и менеджмента и развившая многие идеи управления организациями в условиях неопределенности. Расцвет этого направления в науке приходится на 60-е годы. В 1965 г. президент США Джонсон заявил о необходимости немедленного перехода на новую систему планирования и распределения ресурсов на уровне правительства США, основывающуюся на принципах оптимизации [6, p. vii]. Необходимость выработки формализованного подхода к разработке и принятию решений в условиях неопределенности обусловила появление не только специального аппарата категорий (некоторые из них приведены выше), но и единой теории, логически связывающей эти категории. Основным положением этой теории – теории принятия решений – является утверждение, что лицо, принимающее решение, базируясь на доступной ему информации, выбирает ту альтернативу, которая максимизирует заданное соотношение между свойствами этой альтернативы и некоторым количественным показателем, которым измеряется ее полезность. Однако в условиях неопределенности точной информации о будущем состоянии управляемой системы не существует, поэтому лицо, принимающее решение, моделирует неопределенность, чтобы создать основу для принятия того или иного решения. В теории принятия решений существуют два подхода к моделированию неопределенности; назовем их условно объективный и субъективный. Объективный подход предполагает наличие необходимого объема статистической информации для оценки возможности того или иного события, в предположении о неизменности действия факторов, влияющих на появление этого события. Если каждому возможному событию противопоставить количественную оценку его исхода, такую что, чем выше эта оценка, тем более желаемо событие, ей соответствующее, то наилучшей альтернативой будет та, ожидаемый результат которой будет максимальным, т.е. при которой произведение вероятностей событий, могущих возникнуть при выборе этой альтернативы, на количественные оценки исходов соответствующих событий, максимально[14, 16, 20]. Действие данного принципа иллюстрируется на следующем примере. Пусть принимается решение о закупке релейной системы для использования ее в производственном процессе. Имеется три альтернативы: приобрести и смонтировать систему спецификации 1, стоимостью 10000 ден. ед., 2, стоимостью 12000 ден. ед., или 3, стоимостью 18000 ден. ед. При заводских испытаниях этих систем было получено, что система 1 выходит из строя с вероятностью 0,0016 за сутки, система 2 с вероятностью 0,001 за сутки, система 3 с вероятностью 0,0005 за сутки. Выход системы из строя означает выпуск бракованной продукции на сумму 100000 ден. ед. Необходимо выбрать, какую систему стоит покупать. Объективный подход к принятию решений работает следующим образом. Имеется три альтернативы – купить систему 1, 2 или 3. Затраты, связанные с приобретением системы, делятся на детерминированные (стоимость покупки и монтажа) и неопределенные, или ожидаемые (ожидаемые потери от брака). При ставке дисконтирования 15% в год ожидаемые затраты, связанные с покупкой системы 1 составят 1781,5 ден. ед., системы 2 – 1113,4 ден. ед., системы 3 – 556,7 ден. ед.. Суммарные же затраты составят, соответственно, 11781,5, 13113,4 и 18556,7 ден. ед., поэтому объективный подход в теории принятия решений рекомендует приобрести систему 1, т.к. расходы, связанные с ее покупкой, минимальны. Субъективный подход имеет место потому, что при всей своей простоте объективный подход весьма ограничен по области применения, т.к. далеко не всегда возможно получить достаточно информации о вероятностях тех или иных событий. Кроме того, объективный подход не учитывает факторы более тонкого свойства, такие как отношение лица, принимающего решение, к риску. Например, с точки зрения объективного подхода, сыграть в лотерею стоимостью 4000 ден. ед. с выигрышем в 10000 ден. ед. и вероятностью выигрыша 0,5 выгоднее, чем в лотерею стоимостью 7 ден. ед. с выигрышем в 15 ден. ед. и вероятностью выигрыша 0,6. В самом деле, в первом случае ожидаемый результат составит 10000*0,5 + 0*0,5 – 4000 = 1000 ден. ед., а во втором случае – только 15*0,6 + 0*0,4 – 7 = 2 ден. ед. Однако во многих случаях практики лица, принимающие решения, предпочитают не рисковать по крупному, опасаясь больших потерь в случае неудачи. Этот феномен объясняется, прежде всего, такими факторами, как психологическая склонность к риску, количество доступных денежных средств на момент принятия решения и возможность повторения рисковой ситуации в будущих периодах. Эти факторы объединяются в категории полезности – индивидуальной, субъективной оценки ценности ресурсов, используемых с риском их потери, относительно ожидаемой выгоды или потерь от их использования и имеющегося их количества. Полезность может быть проиллюстрирована функцией полезности. Функция полезности может быть построена от большого числа аргументов, однако для удобства демонстрации метода ограничимся случаем с одним аргументом. Таким аргументом чаще всего бывает доход, прибыль или какой-либо другой финансовый результат от рискового мероприятия. Различные варианты функции полезности показаны на нижеследующем рисунке 1.1. Рис.1.1. Возможные варианты функции полезности Как видно из рисунка, график функции полезности может иметь различный вид: он может быть вогнутой, выпуклой кривой или просто прямой. Специалисты по теории принятия решений используют эти типовые виды функции полезности для иллюстрации отношений лиц, принимающих решения, к риску. Так, вогнутая кривая показывает положительное отношение к риску, азарт, прямая – нейтральное отношение к риску (этот вид кривой полезности описывает объективный подход к принятию решений), выпуклая кривая показывает сдержанное отношение к риску, желание его избежать, даже несмотря на высокие ожидаемые результаты [2, pp. 465-467]. Как показывает практика, наиболее распространенным является третий вариант функции полезности, поэтому представители субъективного подхода в своих исследованиях в основном концентрируются на исследовании функции полезности, иллюстрирующей сдержанное отношение к риску. Функция полезности может строиться двумя путями – непосредственным оцениванием и использованием математической модели как своеобразной заготовки для построения функции полезности. Непосредственное оценивание функции полезности очень трудоемко и может иногда быть противоречивым, поэтому в большинстве случаев используют следующую математическую модель для построения функции полезности [2, p. 477]: где U(x) – функция полезности, R – ее параметр. Параметр R оценивается как максимальная сумма денег, которой бы рискнуло лицо, принимающее решения, чтобы с равными вероятностями выиграть столько же или потерять половину от этой суммы. Полученная функция полезности корректирует процесс принятия решения в соответствии с индивидуальным восприятием риска лицом, принимающим решение. Критерием оптимальности решения в данном случае является не ожидаемый финансовый результат, а ожидаемая полезность финансового результата каждой возможной альтернативы, т.е. альтернатива выбирается исходя из условия: где EUi – ожидаемая полезность i-й альтернативы, pij – вероятность наступления j-го исхода при выборе i-й альтернативы, FRij – финансовый результат j-го исхода i-й альтернативы, U(FRij) – функция полезности от финансового результата. Видно, что для одной и той же альтернативы субъективная категория полезности значительно отличается от объективной категории ожидаемого финансового результата. Это различие основано на психологическом восприятии риска. Математически восприятие риска иллюстрируется категорией премии за риск (или рисковой премии). Рисковая премия – это разность между ожидаемым результатом альтернативы и той суммой денег (или иных ценностей), которую бы лицо, принимающее решение, предпочло получить наверняка, не рискуя. В случае положительного отношения к риску рисковая премия отрицательна, в случае нейтрального отношения к риску – нулевая, в случае сдержанного отношения к риску – положительная. Приведем пример, иллюстрирующий логику субъективного подхода. Пусть задана функция полезности 1) вложить 1500 ден. ед. и получить прибыль в 2000 ден. ед. с вероятностью 0,4, прибыль в 1000 ед. с вероятностью 0,4 и потерять вложенные деньги и получить убыток в 500 ден. ед. с вероятностью 0,2; 2) вложить 2500 ден. ед. и получить прибыль в 3500 ден. ед. с вероятностью 0,3, прибыль в 3000 ед. с вероятностью 0,3 и потерять вложенные деньги с вероятностью 0,4; 3) вложить 500 ден. ед. и получить прибыль в 400 ден. ед. с вероятностью 0,7 и получить вложенные деньги с нулевой прибылью с вероятностью 0,3. Ожидаемые полезности альтернатив следующие: альтернатива 1) (3500)*0,4 + U(2500)*0,4 – U(2000)*0,2 = 0,5384 альтернатива 2) U(6000)*0,3 + U(5500)*0,3 – (2500)*0,4 = 0,2624 альтернатива 3) U(900)*0,7 + U(500)*0,3 = 0,4006 Поэтому выбирается альтернатива 1). Рассчитаем рисковые премии для каждой альтернативы. Ожидаемые результаты альтернатив 1), 2) и 3) равны, соответственно, 2000, 2450 и 2130 ден. ед. Для получения сумм, которые бы лицо, принимающее решение, согласилось получить, не рискуя, для каждой альтернативы решим уравнение:
Для альтернативы 1) получаем, что эта сумма равна 1160 ден. ед., для альтернативы 2) 456,53 ден. ед., для альтернативы 3) 767,7 ден. ед. Поэтому рисковая премия для альтернативы 1) составит 840 ден. ед., для альтернативы 2) 1993,47 ден. ед., для альтернативы 3) 1362,3 ден. ед. Легко заметить, что для оптимальной альтернативы рисковая премия минимальна, что говорит о том, что субъективный подход позволяет получить решение, наиболее рациональным образом сочетающее готовность идти на риск и его ожидаемые последствия. Приведенные выше подходы лишь в общих, принципиальных чертах отражают современное состояние теории принятия решений. В отдельных ее направлениях используются сложные проблемно ориентированные методики: методы теории графов, генетические алгоритмы оптимизации, теорию нечетких множеств, теорию нейросетей и другие области знания, изучить которые можно по специальной литературе. Теория принятия решений в своем современном состоянии способна предложить эффективные решения многих проблем, связанных с управлением организаций в условиях неопределенности. Однако остаются проблемы, в том числе и методологического характера, которые либо не рассматриваются представителями данного направления, либо до сих пор не получили удовлетворительного решения. Одной из таких проблем является увязка оптимального управления в условиях неопределенности с целью функционирования управляемой организации. Дело в том, что оптимизация по параметру, входящему в множество параметров, которыми задается цель, особенно в условиях неопределенности, не представляется полностью корректной. Банальный пример: торговый агент фирмы получил задание добиться максимального объема продаж. Предположим, что максимизация объема продаж является целью его организации в целом. Однако был непогожий день, и он, как и его коллеги, предпочел остаться в офисе и сделать как можно больше звонков потенциальным клиентам. Звонки с предложением товаров и услуг, очевидно, в ряде случаев являются средством, стимулирующим спрос. Поэтому, сделав максимальное количество звонков, торговый агент максимизировал возможный объем продаж за день. Достигнута ли цель? Да. Ведь торговый агент – профессионал, он не будет делать звонки кому и когда придется. Он умеет планировать рабочее время, умеет вести телефонный разговор, наделен другими профессиональными качествами. Поэтому относительно того образа действий, который он выбрал, он максимизировал свой дневной объем продаж. То же самое сделали и его коллеги. Но результат его деятельности, выраженный в деньгах, не всегда будет соответствовать желаемому, и в этом смысле цель не достигнута (см. приведенное выше определение цели). А если бы он, несмотря на погоду, сделал несколько визитов, показал товар лицом, лично поговорил с покупателями, то, очень возможно, он принес бы компании больше денег. Достигается ли цель в этом случае? Неясно. Ведь агент может передвигаться на общественном транспорте и при всем желании может посетить не более, скажем, 10 клиентов за рабочий день. Тогда как менее расторопный агент, имеющий личный автомобиль, легко может объехать 15 и более клиентов. Какой из агентов максимизирует объем продаж, а какой нет, определить невозможно. Кроме того, максимум объема продаж при одних условиях деятельности может быть менее предпочтительнее, чем далекий от оптимального результат при других условиях деятельности. Пусть условия деятельности всех агентов закреплены в их должностных инструкциях. Но и в этом случае говорить о достижении цели, заключающейся в максимизации объема продаж, не приходится. Как можно определить, максимально ли «выкладывается» конкретный торговый агент или нет? Особенно если мы договорились учитывать неопределенность результатов деятельности торговых агентов. Как, следовательно, можно говорить, достигнута цель или нет? Учитывая вышеприведенные доводы, можно заключить, что гораздо логичнее ставить целью достижение определенного уровня объема продаж или каких-либо других показателей. А критерием оптимизации в этом случае может выступать, например, вероятность ее достижения – та альтернатива, при которой вероятность достижения цели максимальна, и будет оптимальной с учетом неопределенности. Вернемся к примеру, иллюстрирующему логику субъективного подхода. Если целью является максимизация дохода пусть даже с учетом индивидуального восприятия риска, то оптимальной является альтернатива 1). Но что если в результате получается убыток, тогда как, например, альтернатива 3) вообще исключает убыток? Получается, что цель не достигнута, а решение принято, на самом деле, неправильно. Пусть вероятность этого события невелика, она все же есть. Конечно, можно сослаться на неопределенность, но представляет интерес по возможности ослабить ее негативное влияние на результат, правильно поставив цель и определив критерий оптимальности альтернативы. Если мы поставим цель получить неотрицательный доход и в качестве критерия выбора оптимальной альтернативы зададим вероятность ее достижения, то оптимальной альтернативой окажется альтернатива 3). При этом мы можем гарантировать достижение цели, несмотря на неопределенность. Однако доход от этой альтернативы даже при самом положительном исходе событий (который нельзя не учитывать) значительно меньше, чем доходы от других альтернатив. Поэтому порог цели можно повысить, при этом, конечно, допуская некоторый риск недостижения поставленной цели. Пусть целью является получение дохода не меньше 5000 ден. ед. Тогда вероятность достижения поставленной цели для альтернатив 1) и 3) будет равна 0, а для альтернативы 2) 0,6; поэтому в данном случае оптимальной альтернативой будет альтернатива 2). А если целью является получение дохода больше 1500 ден. ед. (мы здесь используем параметр функции полезности, учитывая его смысл), оптимальной альтернативой будет альтернатива 1). Таким образом, получаем, что выбор альтернативы зависит от уровня притязаний лица, принимающего решения, и от возможности эти притязания удовлетворить. Это похоже на то, как люди поступают в жизни. Может быть, такую логику стоит использовать при принятии управленческих решений? Исследованию этого вопроса и посвящено дальнейшее изложение работы. Интересно, что исследование операций зародилось в военных лабораториях и сначала было призвано решать проблемы, связанные с распределением ресурсов для боевых действий, разработкой военных стратегий и т.п. |
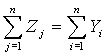
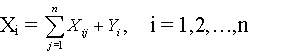 (1.3)
(1.3)