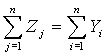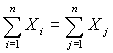Орлов А.И. Основы теории принятия решений: Задачи по курсу "Теория принятия решений"

10. Задачи по курсу "Теория принятия решений"

1. Какой образец мотоцикла запустить в серию? Исходные данные для принятия решения приведены в табл.11. Разберите четыре критерия принятия решения: пессимистичный, оптимистичный, средней прибыли, минимальной упущенной выгоды.

Табл.11. Прибыль фирмы при различном выборе образца мотоцикла для запуска в серию (млн. руб.)

Цена бензина	Мотоцикл "Витязь"	Мотоцикл "Комар"
Низкая (20 % )	900	700
Средняя (60%)	700	600
Высокая (20 % )	100	400

2. Изобразите на плоскости ограничения задачи линейного программирования и решите (графически) эту задачу:

400 W₁ + 450 W₂ → min ,

5 W₁ + 10 W₂ ≥ 45,

20 W₁ + 15 W₂ ≥ 80,

W₁ ≥ 0,

W₂ ≥ 0.

3. Решите задачу линейного программирования:

W₁ + 5 W₂ → max ,

0,1 W₁ + W₂ ≤ 3,8 ,

0,25 W₁ + 0,25 W₂ ≤ 4,2 ,

W₁ ≥ 0 ,

W₂ ≥ 0 .

4. Решите задачу целочисленного программирования:

10 Х + 5 У → max .

8 Х + 3 У ≤ 40,

3 Х + 10 У ≤ 30,

Х ≥ 0 , У ≥ 0 , Х и У - целые числа.

5. Решите задачу о ранце:

Х₁ + Х₂ + 2Х₃ + 2Х₄ + Х₅ + Х₆ → max ,

0,5Х₁ + Х₂ + 1,5Х₃ + 2Х₄ + 2,5Х₅ + 3Х₆ ≤ 3.

Управляющие параметры Х_k , k = 1,2,…,6 , принимают значения из множества, содержащего два элемента - 0 и 1.

6. В табл.12 приведены упорядочения 7 инвестиционных проектов, представленные 7 экспертами.

Табл.12. Упорядочения проектов экспертами

Эксперты	Упорядочения
1	1 < {2,3} < 4 < 5 < {6,7}
2	{1,3} < 4 < 2< 5< 7 < 6
3	1 < 4 < 2 < 3 < 6 < 5 < 7
4	1 < {2, 4} < 3 < 5 < 7 <6
5	2 < 3 < 4 < 5 <1 <6 <7
6	1 < 3 < 2 < 5 < 6 < 7 < 4
7	1 < 5 < 3 < 4 < 2 < 6 < 7

Найдите:
а) итоговое упорядочение по средним арифметическим рангам;
б) итоговое упорядочение по медианам рангов;
в) кластеризованную ранжировку, их согласующую.

7. Выпишите матрицу из 0 и 1, соответствующую бинарному отношению (кластеризованной ранжировке):

5 < {1, 3} < 4 < 2 < {6, 7} .

8. Найдите расстояние Кемени между бинарными отношениями - упорядочениями А = [3< 2 <1< {4,5}] и B = [ 1 < {2 ,3} < 4 < 5 ].

9. Дана квадратная матрица (порядка 9) попарных расстояний для множества бинарных отношений из 9 элементов А₁, А₂, А₃,..., А₉ (табл.13). Найдите в этом множестве медиану для множества из 5 элементов {А₂, А₄, А₅, А₈, А₉}.

Табл.13. Попарные расстояния между бинарными отношениями

0	2	13	1	7	4	10	3	11
2	0	5	6	1	3	2	5	1
13	5	0	2	2	7	6	5	7
1	6	2	0	5	4	3	8	8
7	1	2	5	0	10	1	3	7
4	3	7	4	10	0	2	1	5
10	2	6	3	1	2	0	6	3
3	5	5	8	3	1	6	0	9
11	1	7	8	7	5	3	9	0

10. Решите задачу коммивояжера для четырех городов (маршрут должен быть замкнутым и не содержать повторных посещений). Затраты на проезд приведены в табл.14.

Табл.14. Исходные данные к задаче коммивояжера

Город отправления	Город назначения	Затраты на проезд
А	Б	2
А	В	1
А	Д	5
Б	А	3
Б	В	2
Б	Д	1
В	А	4
В	Б	1
В	Д	2
Д	А	5
Д	Б	3
Д	В	3

11. Транспортная сеть (с указанием расстояний) приведена на рис.9. Найдите кратчайший путь из пункта 1 в пункт 4.

Рис.9. Исходные данные к задаче о кратчайшем пути.

12. Как послать максимальное количество грузов из начального пункта 1 в конечный пункт 8, если пропускная способность путей между пунктами транспортной сети (рис.10) ограничена (табл.15)?

Табл.15. Исходные данные к задаче о максимальном потоке