Прикладная статистика: Принцип инвариантности

Часть 1. Фундамент прикладной статистики

1.4. Теоретическая база прикладной статистики

1.4.5. Принцип инвариантности

Пусть Y₁, Y₂, … , Y_n – независимые одинаково распределенные случайные величины с непрерывной функцией распределения F(x). Многие используемые в прикладной статистике функции от результатов наблюдений выражаются через эмпирическую функцию распределения F_n(x). К ним относятся статистики Колмогорова, Смирнова, омега-квадрат. Отметим, что и другие статистики выражаются через эмпирическую функцию распределения, например:

.

Полезным является преобразование Н.В.Смирнова t = F(x). Тогда независимые случайные величины Z_j = F(Y_j), j = 1, 2, … , n, имеют равномерное распределение на отрезке [0; 1]. Рассмотрим построенную по ним эмпирическую функцию распределения F_n(t), 0 < t < 1. Эмпирическим процессом называется случайный процесс

.

Рассмотрим критерии проверки согласия функции распределения выборки с фиксированной функцией распределения F(x). Статистика критерия Колмогорова записывается в виде

статистика критерия Смирнова – это

а статистика критерия омега-квадрат (Крамера-Мизеса-Смирнова) имеет вид

.

Случайный процесс ξ_n(t) имеет нулевое математическое ожидание и ковариационную функцию Мξ_n(s)ξ_n(t) = min (s,t) – st. Рассмотрим гауссовский случайный процесс ξ(t) с такими же математическим ожиданием и ковариационной функцией. Он называется броуновским мостом. (Напомним, что гауссовским процесс именуется потому, что вектор (ξ(t₁), ξ(t₂), … , ξ(t_k)) имеет многомерное нормальное распределение при любых наборах моментов времени t₁, t₂, … , t_k.)

Пусть f – функционал, определенный на множестве возможных траекторий случайных процессов. Принцип инвариантности [1] состоит в том, что последовательность распределений случайных величин f(ξ_n) сходится при n → ∞ к распределению случайной величины f(ξ). Сходимость по распределению обозначим символом =>. Тогда принцип инвариантности кратко записывается так: f(ξ_n) => f(ξ). В частности, согласно принципу инвариантности статистика Колмогорова и статистика омега квадрат сходятся по распределению к распределениям соответствующих функционалов от случайного процесса ξ:

 => ,  => .

Таким образом, от проблем прикладной статистики сделан переход к теории случайных процессов. Методами этой теории найдены распределения случайных величин

,  .

Принцип инвариантности – инструмент получения предельных распределений функций от результатов наблюдений, используемых в прикладной статистике.

Обоснование принципу инвариантности может быть дано на основе теории сходимости вероятностных мер в функциональных пространствах [8]. Более простой подход, позволяющий к тому же получать необходимые и достаточные условия в предельной теории статистик интегрального типа (принцип инвариантности к ним нельзя применить), рассмотрен в главе 2.3.

Почему «принцип инвариантности» так назван? Обратим внимание, что предельные распределения рассматриваемых статистик не зависят от их функции распределения F(x). Другими словами, предельное распределение инвариантно относительно выбора F(x).

В более широком смысле термин «принцип инвариантности» применяют тогда, когда предельное распределение не зависит от тех или иных характеристик исходных распределений [1]. В этом смысле наиболее известный «принцип инвариантности» - это Центральная Предельная Теорема, поскольку предельное стандартное нормальное распределение – одно и то же для всех возможных распределений независимых одинаково распределенных слагаемых (лишь бы слагаемые имели конечные математическое ожидание и дисперсию).
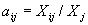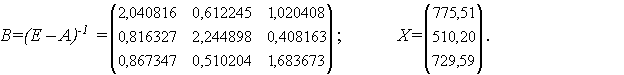